题目内容
已知数列{an}的前n项的和为Sn,a1=-
,an+1=
,则S2015= .
| 1 |
| 2 |
|
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:利用分段数列的定义、数列的周期性即可得出.
解答:
解:∵a1=-
,an+1=
,
∴a2=2a1+1=0,a3=2a2+1=1,
a4=a3-
=
,a5=a4-
=-
.
∴an+4=an.
又a1+a2+a3+a4=-
+0+1+
=
.
∴S2015=(a1+a2+a3)+503×
=
+
=
.
故答案为:
.
| 1 |
| 2 |
|
∴a2=2a1+1=0,a3=2a2+1=1,
a4=a3-
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
∴an+4=an.
又a1+a2+a3+a4=-
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
∴S2015=(a1+a2+a3)+503×
| 3 |
| 4 |
=
| 1 |
| 2 |
| 1509 |
| 4 |
=
| 1511 |
| 4 |
故答案为:
| 1511 |
| 4 |
点评:本题考查了分段数列的定义、数列的周期性,考查了推理能力与计算能力,属于难题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
如图框图属于( )
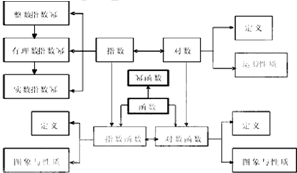

| A、程序框图 | B、工序流程图 |
| C、知识结构图 | D、组织结构图 |
函数f(x)=(x-1)0+
的定义域为( )
| 1 | ||
|
| A、(-3,1) |
| B、(-3,+∞) |
| C、(-3,1)∪(1,+∞) |
| D、(1,+∞) |