题目内容
设a＞b＞0，k＞0且k≠1，则 椭圆C1：
+
=1和 椭圆C2：
+
=k具有相同的（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
分析：由椭圆基本量的平方关系和离心率公式，可算出椭圆C1与椭圆C2的离心率都等于
，而它们的顶点、焦点、和长短轴不一定相同．由此可得本题答案．
| ||
| a |
解答：解：∵椭圆C1：
+
=1中，长半轴为a，短半轴为b，
∴椭圆C1的半焦距c=
，可得椭圆C1的离心率e1=
=
；
将椭圆C2：
+
=k化成标准形式，得C2：
+
=1，
∴k＞0，得椭圆C2的离心率e2=
=
．
因此e1=e2，即椭圆C1与椭圆C2的离心率相同．
当a、b保持不变时椭圆C1的顶点、焦点、长轴和短轴保持不变，
而随着k的变化椭圆C2的顶点、焦点、长轴和短轴都在变化．
因此，两个椭圆不一定有相同的顶点、焦点、和长短轴．
故选：C
| x2 |
| a2 |
| y2 |
| b2 |
∴椭圆C1的半焦距c=
| a2-b2 |
| c |
| a |
| ||
| a |
将椭圆C2：
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2k |
| y2 |
| b2k |
∴k＞0，得椭圆C2的离心率e2=
| ||
a
|
| ||
| a |
因此e1=e2，即椭圆C1与椭圆C2的离心率相同．
当a、b保持不变时椭圆C1的顶点、焦点、长轴和短轴保持不变，
而随着k的变化椭圆C2的顶点、焦点、长轴和短轴都在变化．
因此，两个椭圆不一定有相同的顶点、焦点、和长短轴．
故选：C
点评：本题给出两个形状相同的椭圆，寻找它们的共同性质．着重考查了椭圆的定义、标准方程与简单几何性质等知识，属于基础题．
练习册系列答案
课堂全解字词句段篇章系列答案
相关题目
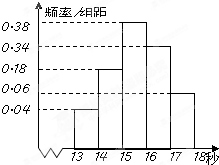（2011•西山区模拟）为调查某市学生百米运动成绩，从该市学生中按照男女生比例随机抽取50名学生进行百米测试，学生成绩全部都介于13秒到18秒之间，将测试结果按如下方式分成五组，第一组[13，14），第二组[14，15）…第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．
(a>b>0)的一个焦点到长轴的两个端点的距离分别为
。
（a，b＞0）的左、右焦点分别为F1，F2，若P 是椭圆上的一点，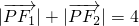
，离心率
．
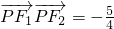，求点P的坐标；
（a，b＞0）的左、右焦点分别为F1，F2，若P 是椭圆上的一点，
，离心率
．
，求点P的坐标；