题目内容
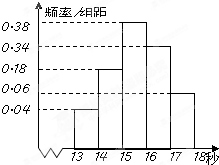 (2011•西山区模拟)为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
(2011•西山区模拟)为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.| 性别 是否 达标 |
男 | 女 | 合计 |
| 达标 | a=24 | b= 6 6 |
30 30 |
| 不达标 | c= 8 8 |
d=12 | 20 20 |
| 合计 | 32 32 |
18 18 |
n=50 |
(Ⅱ) 根据有关规定,成绩小于16秒为达标.
如果男女生使用相同的达标标准,则男女生达标情况如附表:
根据上表数据,能否有99%的把握认为“体育达标与性别有关”?若有,你能否提出一个更好的解决方法来?
附:K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥K) | 0.050 | 0.010 | 0.001 |
| K | 3.841 | 6.625 | 10.828 |
分析:(I)成绩在[13,14)的人数有2人,设为a,b.成绩在[17,18]的人数有3人,设为A,B,C;基本事件总数为10,事件“|m-n|>2”由6个基本事件组成.根据古典概型公式可求出所求.
(Ⅱ)根据列联表所给的数据,代入随机变量的观测值公式,得到观测值的结果,把观测值的结果与临界值进行比较,即可求得.
(Ⅱ)根据列联表所给的数据,代入随机变量的观测值公式,得到观测值的结果,把观测值的结果与临界值进行比较,即可求得.
解答: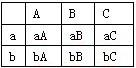 解:(Ⅰ)成绩在[13,14)的人数有:50×0.04=2人,设为a,b.
解:(Ⅰ)成绩在[13,14)的人数有:50×0.04=2人,设为a,b.
成绩在[17,18]的人数有:50×0.06=3人,
设为A,B,C.m,n∈[13,14)时有ab一种情况.
m,n∈[17,18]时有AB,AC,BC三种情况.
m,n分别在[13,14)和[17,18]时有aA,aB,aC,bA,bB,bC六种情况.
基本事件总数为10,事件“|m-n|>2”由6个基本事件组成.
所以P(|m-n|>2)=
=
(13分)…(6分)
(Ⅱ)依据题意得相关的2×2列列联表联表如下:
…(9分)
K2=
≈8.333>6.625,
故有99%的把握认为“体育达标与性别有关”
故可以根据男女生性别划分达标的标准…(12分)
 解:(Ⅰ)成绩在[13,14)的人数有:50×0.04=2人,设为a,b.
解:(Ⅰ)成绩在[13,14)的人数有:50×0.04=2人,设为a,b.成绩在[17,18]的人数有:50×0.06=3人,
设为A,B,C.m,n∈[13,14)时有ab一种情况.
m,n∈[17,18]时有AB,AC,BC三种情况.
m,n分别在[13,14)和[17,18]时有aA,aB,aC,bA,bB,bC六种情况.
基本事件总数为10,事件“|m-n|>2”由6个基本事件组成.
所以P(|m-n|>2)=
| 6 |
| 10 |
| 3 |
| 5 |
(Ⅱ)依据题意得相关的2×2列列联表联表如下:
| 性别 是否达标 |
男 | 女 | 合计 |
| 达标 | a=24 | b=6 | 30 |
| 不达标 | c=8 | d=12 | 20 |
| 合计 | 32 | 18 | n=50 |
K2=
| 50×(24×12-6×8)2 |
| 32×18×30×20 |
故有99%的把握认为“体育达标与性别有关”
故可以根据男女生性别划分达标的标准…(12分)
点评:本题主要考查了独立性检验的应用、频率分布直方图,以及古典概型的概率问题、用样本的数字特征估计总体的数字特征等有关知识,属于中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
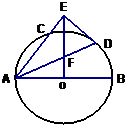 (2011•西山区模拟)如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于D,DE⊥AC交AC延长线于点E,OE交AD于点F.
(2011•西山区模拟)如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于D,DE⊥AC交AC延长线于点E,OE交AD于点F.