题目内容
已知在正方体ABCD—A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG=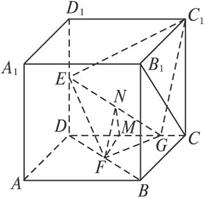
(1)求证:EF⊥B1C;
(2)求二面角FEGC1的大小(用反三角函数表示).
解法一:(1)证明:连结D1B、BC1,∵E、F是D1D、BD的中点,
∴EF∥D1B,且EF=![]() D1B.又∵D1C1⊥平面BC1,
D1B.又∵D1C1⊥平面BC1,
∴D1B在平面BC1上的射影为BC1.
∵BC1⊥B1C,由三垂线定理知B1C⊥D1B.
∴EF⊥B1C.
(2)取DC的中点M,连结FM,则FM⊥DC.过M作MN⊥EG于N点,连结FN.

由三垂线定理可证FN⊥EG.
∴∠MNF的邻补角为二面角FEGC1的平面角.设正方体的棱长为4,则FM=2,
在Rt△EDG中,△EDG∽△MNG,
∴MN=![]() .
.
在Rt△FMN中,∠MNF=90°,
∴tan∠MNF=![]() =
=![]() .
.
∴∠MNF=arctan![]() .
.
∴二面角F-EG-C1的大小为π-arctan![]() .
.
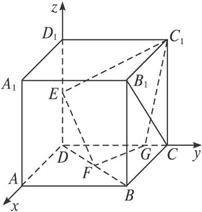
解法二:建立如图直角坐标系,令AB=4,则D(0,0,0),A(4,0,0),B(4,4,0),C(0,4,0),D1(0,0,4),C1(0,4,4),E(0,0,2),F(2,2,0),G(0,3,0),B1(4,4,4).
(1)![]() =(2,2,-2),
=(2,2,-2),![]() =(-4,0,-4).
=(-4,0,-4).
∵![]() ·
·![]() =0,∴EF⊥B1C.
=0,∴EF⊥B1C.
(2)设平面FEG的法向量为n1=(x1,y1,z1),平面C1EG的法向量n2=(1,0,0),
![]() =(2,2,-2),
=(2,2,-2),![]() =(0,3,-2),
=(0,3,-2),![]() ·n1=2x1+2y1-2z1=0,
·n1=2x1+2y1-2z1=0,
EG·n1=3y1-2z1=0,∴n1=(1,2,3), cosθ=![]() .
.
故二面角FEGC1的大小为π-arccos![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 已知在正方体ABCD-A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG=
已知在正方体ABCD-A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG= 已知在正方体ABCD-A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG=
已知在正方体ABCD-A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG=

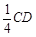 .
. 