题目内容
如图，设△ABC三条边的中线AD、BE、CF相交于点G，则下列三个向量：| AB |
| BC |
| CA |
| GA |
| GB |
| GC |
| BF |
| DC |
| AE |
分析：由△ABC三条边的中线AD、BE、CF相交于点G，结合图形知
+
+
=
，
+
+
=-
+
=
，
+
+
=
(
+
+
)≠
．
| AB |
| BC |
| CA |
| 0 |
| GA |
| GB |
| GC |
| GC |
| GC |
| 0 |
| BF |
| DC |
| AE |
| 1 |
| 2 |
| BA |
| AC |
| BC |
| 0 |
解答：解：∵△ABC三条边的中线AD、BE、CF相交于点G，
∴
+
+
=
，
+
+
=-
+
=
，
+
+
=
(
+
+
)≠
，
∴三个向量：
+
+
，
+
+
，
+
+
中，
等于零向量的有2个．
故选B．
∴
| AB |
| BC |
| CA |
| 0 |
| GA |
| GB |
| GC |
| GC |
| GC |
| 0 |
| BF |
| DC |
| AE |
| 1 |
| 2 |
| BA |
| AC |
| BC |
| 0 |
∴三个向量：
| AB |
| BC |
| CA |
| GA |
| GB |
| GC |
| BF |
| DC |
| AE |
等于零向量的有2个．
故选B．
点评：本题考查向量的加减法混合运算及其几何意义，是基础题．解题时要认真审题，注意数形结合思想的灵活运用．
练习册系列答案
阅读快车系列答案
相关题目
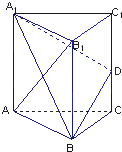如图，已知三棱柱ABC-A1B1C1的所有棱长都相等，且侧棱垂直于底面，由B沿棱柱侧面经过棱C C1到点A1的最短路线长为2
如图，在正三棱柱ABC-A1B1C1中，AB=3，AA1=4，M为AA1的中点，P是BC上一点，且由P沿棱柱侧面经过棱CC1到M的最短路线长为
，
中，等于零向量的有（ ）