Question

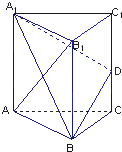如图，已知三棱柱ABC-A₁B₁C₁的所有棱长都相等，且侧棱垂直于底面，由B沿棱柱侧面经过棱C C₁到点A₁的最短路线长为2

5

，设这条最短路线与CC₁的交点为D．
（1）求三棱柱ABC-A₁B₁C₁的体积；
（2）在平面A₁BD内是否存在过点D的直线与平面ABC平行？证明你的判断；
（3）证明：平面A₁BD⊥平面A₁ABB₁．

Answer 1

分析：（1）由题意求出棱长，再求出三棱柱ABC-A₁B₁C₁的底面面积，再求出高AA₁，即可求出棱柱的体积．
（2）设A₁B与AB₁的交点为O，连接BB₂，OD，在平面A₁BD内存在过点D的直线OD与平面ABC内的直线BB₂平行，即可证明所要证明结论．
（3）连接AD，B₁D，平面A₁BD内的直线OD垂直平面A₁ABB₁内的两条相交直线A₁B，AB₁，即可证明平面A₁BD⊥平面A₁ABB₁．

解答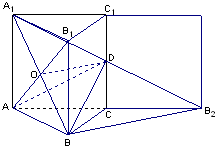：解：（1）如图，将侧面BB₁C₁C绕棱CC₁旋转120°
使其与侧面AA₁C₁C在同一平面上，点B运动到点B₂的位置，
连接A₁B₂，则A₁B₂就是由点B沿棱柱侧面经过棱CC₁到点A₁的最短路线．
设棱柱的棱长为a，则B₂C=AC=AA₁=a，
∵CD∥AA₁∴D为CC₁的中点，（1分）
在Rt△A₁AB₂中，由勾股定理得A₁A²+AB₂²=A₁B₂²，
即 a²+4a²=(2

5

)2解得a=2，（3分）
∵S△ABC=

3

4

×22 =

3

∴VABC-A1 B1C1=S△ABC•AA1=2

3

（4分）
（2）设A₁B与AB₁的交点为O，连接BB₂，OD，则OD∥BB₂（6分）
∵BB₂?平面ABC，OD不在平面ABC
∴OD∥平面ABC，
即在平面A₁BD内存在过点D的直线与平面ABC平行（8分）
（3）连接AD，B₁D
∵Rt△A₁C₁D≌Rt△BCD≌Rt△ACD
∴A₁D=BD=B₁D=AD∴OD⊥A₁B，OD⊥AB₁（10分）
∵A₁B∩AB₁=O∴OD⊥平面A₁ABB₁
又∵OD?平面A₁BD∴平面A₁BD⊥平面A₁ABB₁．（12分）

点评：本题考查组合几何体的面积、体积问题，棱柱的结构特征，空间中直线与平面之间的位置关系，平面与平面垂直的判定，考查空间想象能力，逻辑思维能力，是中档题．