题目内容
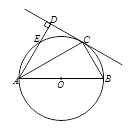
如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交于BC于点E,AB=2AC.
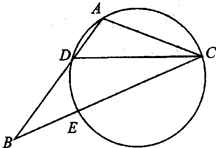
(Ⅰ)求证:BE=2AD;
(Ⅱ)当AC=1,EC=2时,求AD的长.

(Ⅰ)求证:BE=2AD;
(Ⅱ)当AC=1,EC=2时,求AD的长.
(Ⅰ)详见解析;(Ⅱ) .
.
 .
.试题分析:(Ⅰ)要证明
 ,注意到
,注意到 是
是 的平分线,等角对等弦,可连接
的平分线,等角对等弦,可连接 ,则
,则 ,可证
,可证 ,又因为
,又因为 ,可证
,可证 即可,由圆内接四边形的性质可证;(Ⅱ)根据割线定理,建立
即可,由圆内接四边形的性质可证;(Ⅱ)根据割线定理,建立 的方程,解出
的方程,解出 即可.
即可.试题解析:(Ⅰ)连接
 ,因为
,因为 是圆的内接四边形,所以
是圆的内接四边形,所以 ,又
,又 ,所以
,所以 ,即有
,即有 ,又
,又 ,所以
,所以 ,又
,又 是
是 的平分线,
的平分线,所以
 ,从而
,从而 .
.
(Ⅱ)由条件的
 设
设 ,根据割线定理得
,根据割线定理得 ,即
,即 ,所以
,所以 即
即
解得
 ,或
,或 (舍去),即
(舍去),即

练习册系列答案
相关题目
 是⊙
是⊙ 的直径,弦
的直径,弦 的延长线相交于点
的延长线相交于点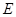 ,
, 垂直
垂直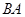 的延长线于点
的延长线于点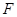 .
.
 ;
;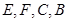 四点共圆.
四点共圆. 与圆
与圆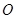 相切于点
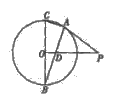
相切于点 ,直径
,直径  ,连结
,连结 交
交 于点
于点 .
.
 ;
;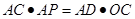 .
. 均在⊙O上,且
均在⊙O上,且 为⊙O的直径。
为⊙O的直径。 的值;
的值; ,
, 与
与 交于点
交于点 ,且
,且 、
、 为弧
为弧 的三等分点,求
的三等分点,求 的长.
的长.
 ,
, ,则
,则 的最小值为( )
的最小值为( )



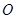 的直径
的直径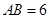 ,
,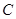 为圆周上一点,
为圆周上一点,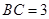 ,过
,过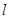 ,过
,过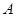 作
作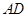 ,垂足为
,垂足为 .
.
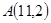 作圆
作圆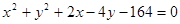 的弦,其中弦长为整数的共有( )
的弦,其中弦长为整数的共有( ) 是直线
是直线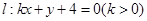 上一动点,
上一动点, 是圆
是圆 的两条切线,切点分别为
的两条切线,切点分别为 .若四边形
.若四边形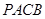 的最小面积为2,则
的最小面积为2,则 = .
= . 是⊙
是⊙ 的直径,
的直径, 是
是 ,
, ,若
,若 ,则⊙
,则⊙
