题目内容
【题目】在直角坐标系![]() 中,设椭圆
中,设椭圆![]() 的焦点为
的焦点为![]() ,过右焦点
,过右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,若
两点,若![]() 的周长为短轴长的
的周长为短轴长的![]() 倍.
倍.
(Ⅰ)求椭圆![]() 的离心率;
的离心率;
(Ⅱ)设![]() 的斜率为
的斜率为![]() ,在椭圆
,在椭圆![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标.
的坐标.
【答案】(1)![]() (2)不存在点
(2)不存在点![]() ,使
,使![]() 成立.
成立.
【解析】试题分析:(1)根据椭圆定义得![]() 的周长为
的周长为![]() ,即
,即![]() ,解得椭圆
,解得椭圆![]() 的离心率;(2)设
的离心率;(2)设![]() ,
, ![]() ,
, ![]() ,则由
,则由![]() 得
得![]() 代入等式
代入等式![]() ,并化简得
,并化简得![]() .利用直线方程
.利用直线方程![]() 与椭圆方程联立方程组,结合韦达定理得
与椭圆方程联立方程组,结合韦达定理得![]() ,
, ![]() .代入解得矛盾,故不存在.
.代入解得矛盾,故不存在.
试题解析:解:(Ⅰ)∵椭圆![]() :
: ![]() 的焦点为
的焦点为![]() ,
, ![]() ,
,
过右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,
两点,
![]() 的周长为短轴长的
的周长为短轴长的![]() 倍,
倍, ![]() 的周长为
的周长为![]() .
.
∴依题意知![]() ,即
,即![]() .
.
∴椭圆![]() 的离心率
的离心率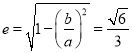 .
.
(Ⅱ)设椭圆方程为![]() ,
,
直线的方程为![]() ,
,
代入椭圆方程得![]() .
.
设![]() ,
, ![]() ,
,
则![]() ,
, ![]() .
.
设![]() ,则
,则![]() .①
.①
由![]() 得
得![]()
代入①得![]() .
.
因为![]() ,
, ![]() ,
,
所以![]() .②
.②
而![]()
![]() .
.
从而②式不成立.
故不存在点![]() ,使
,使![]() 成立.
成立.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


