题目内容

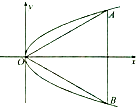
【题目】已知点F1 ， F2分别是双曲线 的左、右焦点，过F1且垂直于x轴的直线与双曲线交于A，B两点，若△ABF2是锐角三角形，则该双曲线离心率的取值范围是（ ）
A.
B.
C.
D.

【答案】D
【解析】解：在双曲线 中，
令x=﹣c 得，y=± ，∴A，B两点的纵坐标分别为± ．
由△ABF2是锐角三角形知，∠AF2F1＜ ，tan∠AF2F1= ＜tan =1，
∴ ＜1，c2﹣2ac﹣a2＜0，e2﹣2e﹣1＜0，∴1﹣ ＜e＜1+ ．
又 e＞1，∴1＜e＜1+ ，
故选D．
先求出A，B两点的纵坐标，由△ABF2是锐角三角形知，tan∠AF2F1= ＜1，e2﹣2e﹣1＜0，解不等式求出e 的范围．

练习册系列答案
相关题目

【题目】如图，等边三角形OAB的边长为8 ，且三个顶点均在抛物线E：y2=2px（p＞0）上，O为坐标原点．

（1）证明：A、B两点关于x轴对称；
（2）求抛物线E的方程．

【题目】如图，在棱长为2 的正方体ABCD﹣A1B1C1D1中，M是A1B1的中点，点P是侧面CDD1C1上的动点，且MP∥截面AB1C，则线段MP长度的取值范围是（ ）

A.
B.
C.
D.

【题目】过点M（﹣2，0）的直线l与椭圆x2+2y2=2交于P1 ， P2 ， 线段P1P2的中点为P．设直线l的斜率为k1（k1≠0），直线OP的斜率为k2 ， 则k1k2等于（ ）
A.﹣2
B.2
C.
D.﹣

【题目】若| |=1，| |=m，| + |=2．
（1）若| +2 |=3，求实数m的值；
（2）若 + 与 ﹣ 的夹角为 ，求实数m的值．

【题目】已知函数f（x）= ﹣1+lnx，若存在x0＞0，使得f（x0）≤0有解，则实数a的取值范围为 ．

【题目】已知函数f（x）=x3+ax2+bx图象与直线x﹣y﹣4=0相切于（1，f（1））
（1）求实数a，b的值；
（2）若方程f（x）=m﹣7x有三个解，求实数m的取值范围．

【题目】已知函数 ，θ∈[0，2π）
（1）若函数f（x）是偶函数：①求tanθ的值；②求 的值．
（2）若f（x）在 上是单调函数，求θ的取值范围．

【题目】已知椭圆C： + =1（a＞b＞0）的左、右焦点分别为F1、F2 ， 点M（0，2）关于直线y=﹣x的对称点在椭圆C上，且△MF1F2为正三角形．
（1）求椭圆C的方程；
（2）垂直于x轴的直线与椭圆C交于A，B两点，过点P（4，0）的直线PB交椭圆C于另一点E，证明：直线AE与x轴相交于定点．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网