题目内容
选修4—5:不等式选讲
设函数 =
=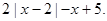
(I)求函数 的最小值m;
的最小值m;
(II)若不等式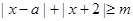 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
(I) (II)
(II) 或
或
解析试题分析:(Ⅰ)
显然,函数 在区间
在区间 上单调递减,在区间
上单调递减,在区间 上单调递增,
上单调递增,
所以函数 的最小值
的最小值
(Ⅱ)由(Ⅰ)知 ,
,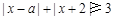 恒成立,
恒成立,
由于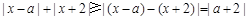 ,
,
等号当且仅当 时成立,故
时成立,故 ,解之得
,解之得 或
或
所以实数 的取值范围为
的取值范围为 或
或
考点:函数的最值 不等式恒成立
点评:利用绝对值的性质化简函数,是求函数最值得关键,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 ,证明函数
,证明函数 在
在 上单调递增;
上单调递增; .
.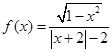 (2)
(2)
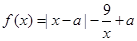 ,
, ,
,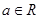 .
.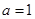 ,试判断并证明函数
,试判断并证明函数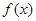 的单调性;
的单调性;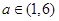 时,求函数
时,求函数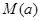 .
.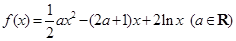 .
. 在
在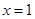 和
和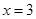 处的切线互相平行,求
处的切线互相平行,求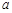 的值;
的值; 的单调区间;
的单调区间;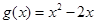 ,若对任意
,若对任意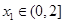 ,均存在
,均存在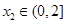 ,使得
,使得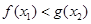 ,求
,求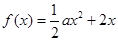 ,
, .
.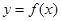 在
在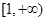 上是单调减函数,求
上是单调减函数,求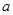 的取值范围;
的取值范围; ,使得方程
,使得方程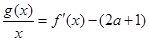 在区间
在区间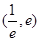 内有且只有两个不相等的实数根?若存在,请求出
内有且只有两个不相等的实数根?若存在,请求出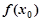 是函数
是函数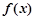 在点
在点 附近的某个局部范围内的最大(小)值,则称
附近的某个局部范围内的最大(小)值,则称 ,函数
,函数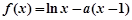 .
. ,求函数
,求函数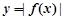 的极值点;
的极值点;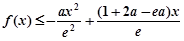 恒成立,求
恒成立,求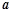 的取值范围.
的取值范围.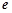 为自然对数的底数)
为自然对数的底数) ,
,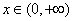 ,是否存在实数
,是否存在实数 ,使
,使 同时满足下列两个条件:(1)
同时满足下列两个条件:(1) 上是减函数,在
上是减函数,在 上是增函数;(2)
上是增函数;(2) ,若存在,求出
,若存在,求出 (
( ≠0)在区间(-1,1)上的单调性。
≠0)在区间(-1,1)上的单调性。