题目内容
15.在一次耐力和体能测试之后,组织者对甲、乙、丙、丁四位受测男生的耐力成绩(X)和体能成绩(Y)进行了回归分析,求得回归直线方程为$\stackrel{∧}{y}$=1.5x-3.5.由于某种原因,成绩表(如表所示)中缺失男生乙的耐力和体能成绩.| 甲 | 乙 | 丙 | 丁 | |
| 耐力成绩(X) | 7.5 | m | 8 | 8.5 |
| 体能成绩(Y) | 8 | n | 8.5 | 9.5 |
| 体质成绩(X+Y) | 15.5 | 16 | 16.5 | 18 |
(2)若体质成绩不低于16分者可定为“体质健康优秀”,肺活量成绩不低于3600ml者可定为“心肺功能优秀”,现有5名男生接受了肺活量测试,测试成绩统计得到如下的2×2列联表:
| 体质健康优秀 | 体质健康不优秀 | 总计 | |
| 心肺功能优秀 | 18 | 9 | 27 |
| 心肺功能不优秀 | 8 | 15 | 23 |
| 总计 | 26 | 24 | 50 |
(注:K2=$\frac{n(ad-bc)^{2}}{(a+b)(a+c)(c+d)(b+d)}$)
附表:
| P(K2>k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.076 | 3.841 | 5.024 |
分析 (1)求出$\overline{X}$,$\overline{y}$,代人回归直线方程中得m与n的关系,再利用m+n=16,列出方程组求出m、n的值;
(2)根据表中数据,计算K2,对照数表即可得出结论.
解答 解:(1)根据题意,得;$\overline{X}$=$\frac{1}{4}$(7.5+m+8+8.5)=$\frac{m}{4}$+6,
$\overline{y}$=$\frac{1}{4}$(8+n+8.5+9.5)=$\frac{n}{4}$+6.5,
代人回归直线方程$\stackrel{∧}{y}$=1.5x-3.5中,
得$\frac{n}{4}$+6.5=1.5($\frac{m}{4}$+6)-3.5①;
又m+n=16②,
由①②组成方程组,解得m=8,n=8;
(2)根据表中数据,计算得
K2=$\frac{n(ad-bc)^{2}}{(a+b)(a+c)(c+d)(b+d)}$=$\frac{50{×(18×15-8×9)}^{2}}{27×23×26×24}$≈5.059>3.841,
对照数表得,有95%把握认为:“体质健康优秀”与肺活量高低有关系.
点评 本题考查了回归直线方程与独立性检验的应用问题,是基础题目.

练习册系列答案
相关题目
5.sin14°cos74°-cos14°sin74°=( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}$ |
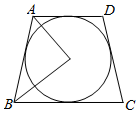 一个圆内切于一个等腰锑形,已知圆面积是等腰锑形面积的$\frac{1}{2}$,求等腰梯形的底角(用反正切表示)
一个圆内切于一个等腰锑形,已知圆面积是等腰锑形面积的$\frac{1}{2}$,求等腰梯形的底角(用反正切表示)