题目内容
10. 一个正四面体木块如图所示,点P是棱VA的中点,过点P将木块锯开,使截面平行于棱VB和AC,若木块的棱长为a,则截面面积为$\frac{a2}{4}$.
一个正四面体木块如图所示,点P是棱VA的中点,过点P将木块锯开,使截面平行于棱VB和AC,若木块的棱长为a,则截面面积为$\frac{a2}{4}$.
分析 利用线面平行的判定定理可得四边形PDEF为所求的截面,易知四边形PDEF为边长为$\frac{1}{2}$a的正方形,问题得以解决.
解答  解:在平面VAC内作直线PD∥AC,交VC于D,
解:在平面VAC内作直线PD∥AC,交VC于D,
在平面VBA内作直线PF∥VB,交AB于F,
过点D作直线DE∥AC,交BC于E,
∵PF∥DE,
∴P,D,E,F四点共面,且面PDEF与VB和AC度平行,
则四边形PDEF为边长为$\frac{1}{2}$a的正方形,
故其面积为$\frac{{a}^{2}}{4}$.
故答案为:$\frac{{a}^{2}}{4}$
点评 本题主要考查线面平行的判定和实际应用,关键之作出截面,属于基础题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
15.曲线f(x)=exlnx+$\frac{{2{e^{x-1}}}}{x}$在点(1,f(1))处的切线方程为( )
| A. | ex-y+2-e=0 | B. | ex+y+2-e=0 | C. | ex-y+2+e=0 | D. | ex+y+2+e=0 |
2.已知a=3${\;}^{\frac{1}{3}}$,b=log${\;}_{\frac{1}{2}}$3,c=log${\;}_{\frac{1}{3}}$$\frac{1}{2}$,则( )
| A. | a>b>c | B. | a>c>b | C. | c>b>a | D. | b>a>c |
20.下列各图中,可表示函数y=f(x)的图象的只可能是( )
| A. | 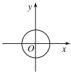 | B. | 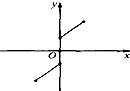 | C. |  | D. | 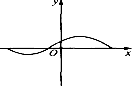 |