题目内容
19.已知f($\frac{x}{2}$-1)=2x+3,且f(m)=6,则m=-$\frac{1}{4}$.分析 设$\frac{x}{2}-1=t$,则x=2t+2,从而f(t)=4t+7,由此能求出结果.
解答 解:∵f($\frac{x}{2}$-1)=2x+3,
设$\frac{x}{2}-1=t$,则x=2t+2,
∴f(t)=4t+7,
∵f(m)=6,
∴4m+7=6,解得m=-$\frac{1}{4}$.
故答案为:$-\frac{1}{4}$.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.若$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(-1,1),(2$\overrightarrow{a}$+$\overrightarrow{b}$)∥($\overrightarrow{a}$-m$\overrightarrow{b}$),则m=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -2 | D. | -$\frac{1}{2}$ |
7.若定义在R上的函数f(x)满足f(0)=-1,f($\frac{1}{m-1}$)<$\frac{1}{m-1}$,其导函数f′(x)满足f′(x)>m,且当x∈[-π,π]时,函数g(x)=-sin2x-(m+4)cosx+4有两个不相同的零点,则实数m的取值范围是( )
| A. | (-∞,-8) | B. | (-∞,-8]∪(0,1) | C. | (-∞,-8]∪[0,1] | D. | (-8,1) |
11.已知函数f(x)=log${\;}_{\frac{2}{3}}}$(x2-2x-3),给定区间E,对任意x1,x2∈E,当x1<x2时,总有f(x1)<f(x2),则下列区间可作为E的是( )
| A. | (-3,-1) | B. | (-1,0) | C. | (1,2) | D. | (3,6) |
9.下列函数,在区间(0,1)上为增函数的是( )
| A. | y=1-x | B. | y=-|x| | C. | $y=\frac{1}{x-1}$ | D. | $y={x^{\frac{1}{2}}}$ |
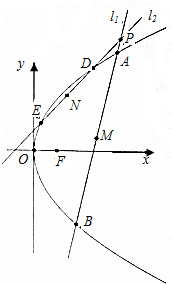 已知抛物线C:y2=2px(p>0)的焦点为F,定点P(3,4)到焦点F的距离为2$\sqrt{5}$且线段PF与抛物线C有公共点,过点P的动直线l1,l2的斜率分别为k1,k2,且满足k1+k2=4,若l1交抛物线C于A,B两点,l2交抛物线C于D,E两点,弦AB,DE的中点分别为M,N.
已知抛物线C:y2=2px(p>0)的焦点为F,定点P(3,4)到焦点F的距离为2$\sqrt{5}$且线段PF与抛物线C有公共点,过点P的动直线l1,l2的斜率分别为k1,k2,且满足k1+k2=4,若l1交抛物线C于A,B两点,l2交抛物线C于D,E两点,弦AB,DE的中点分别为M,N.