题目内容
8．国庆节放假，2个三口之家结伴乘火车外出，每人均实名购票，上车后随意坐所购票的6个座位，则恰好有2人是对号入座（座位号与自己车票相符）的坐法有135种？（用具体数字作答）分析 根据题意，分2步进行分析：首先在在6个人中任取2人，使其对号入座，利用组合数公式计算可得其情况数目，其次分析不是对号入座的4人，假设这4人为A、B、C、D，利用列举法分析可得情况数目，进而由分步计数原理计算可得答案．
解答 解：根据题意，6人中恰好有2人是对号入座，需要在6个人中任取2人，使他的座位号与自己车票相符，有C62=15种坐法，
另外的4人不是对号入座，假设这4人为A、B、C、D，
其座位号与自己车票都不相符的坐法有：BADC，CADB，DABC，BDAC，CDAB，DCAB，BCDA，DCBA，CDBA；共9种坐法，
故6人中恰好有2人是对号入座的坐法有15×9=135种；
故答案为：135．
点评 本题考查排列、组合的应用，涉及错位排序的问题，如果需要分类讨论，务必做到不重不漏．
练习册系列答案
相关题目
16．五种不同商品在货架上排成一排，其中A，B两种必须连排，而C，D两种不能连排，则不同的排法共有（ ）
| A． | 48种 | B． | 24种 | C． | 20种 | D． | 12种 |
3．
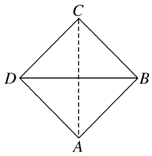已知正四面体（所有棱长都相等的三棱锥）的俯视图如图所示，其中四边形ABCD是边长为$\sqrt{2}$cm的正方形，则这个正四面体的主视图的面积为（ ）cm2．
已知正四面体（所有棱长都相等的三棱锥）的俯视图如图所示，其中四边形ABCD是边长为$\sqrt{2}$cm的正方形，则这个正四面体的主视图的面积为（ ）cm2．| A． | 1 | B． | $\sqrt{2}$ | C． | 2 | D． | 2$\sqrt{2}$ |
13．在圆x2+y2=5x内，过点 （${\frac{5}{2}$，$\frac{3}{2}}$）有n条弦的长度成等差数列，最小弦长为数列的首项a1，最大弦长为an，若公差d∈[${\frac{1}{6}$，$\frac{1}{3}}$]，那么n的取值集合为（ ）
| A． | {4，5，6，7} | B． | {4，5，6} | C． | {3，4，5，6} | D． | {3，4，5，6，7} |
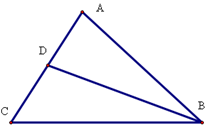在△ABC中，角A、B、C所对的边分别为a，b，c，B=45°，AC=$\sqrt{5}$，cosC=$\frac{{\sqrt{5}，}}{5}$，求