题目内容

函数y=1-2sin2x是（　　）
A、最小正周期为π的奇函数
B、最小正周期为π的偶函数
C、最小正周期为2π的奇函数
D、最小正周期为2π的偶函数
考点：三角函数的周期性及其求法,二倍角的余弦
专题：三角函数的求值
分析：函数解析式利用二倍角的余弦函数公式化简，找出ω的值，代入周期公式求出最小正周期，判断函数奇偶性即可．
解答： 解：y=1-2sin2x=cos2x，
∵ω=2，∴T=
2π
2
=π，
∵余弦函数为偶函数，
∴函数为最小正周期为π的偶函数．
故选：B．
点评：此题考查了三角函数的周期性及其求法，余弦函数的奇偶性，以及二次角的余弦函数公式，熟练掌握公式是解本题的关键．
练习册系列答案
相关题目
给出下列命题：
①若函数f（x）=asinx+cosx的一个对称中心是(
π
6
，0)，则a的值等于-
3
；
②函数f（x）=cos（2x+
π
2
）在区间[0，
π
2
]上单调递减；
③若函数f(x)=sin(2x+
π
3
)的图象向左平移a（a＞0）个单位后得到的图象与原图象关于直线x=
π
2
对称，则a的最小值是
π
6
；
④已知函数f（x）=sin（2x+ϕ） （-π＜ϕ＜π），若-|f（
π
6
）|≤f（x） 对任意x∈R恒成立，则：φ=
π
6
或-
5π
6
．
其中正确结论的序号是
 
．
下面是一些命题的叙述语，其中命题和叙述方法都正确的是
 
．
（1）∵A∈α，B∈α，∴AB∈α．
（2）∵a∈α，α∈β，∴α∩β=a．
（3）∵A∈a，a?α，∴A∈α．
（4）∵A?a，a?α，∴A?α．
点P（x，y）为不等式组
x2+y2≤1
x-y-1≤0
x+y+1≥0
表示的平面区域上一点，则x+2y取值范围为（　　）
A、[-
5
，
5
]
B、[-2，
5
]
C、[-1，2]
D、[-2，2]
已知等比数列{an}的前n项积为Πn，若a3•a4•a8=8，则Π9=（　　）
A、512B、256
C、81D、16
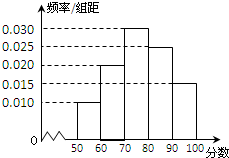某中学从某次考试成绩中抽取若干名学生的分数，并绘制成如图的频率分布直方图．样本数据分组为[50，60），[60，70），[70，80），[80，90），[90，100]．若用分层抽样的方法从样本中抽取分数在[80，100]范围内的数据16个，则其中分数在[90，100]范围内的样本数据有（　　）
A、5个B、6个C、8个D、10个
已知f（x）=2
3
sinx•cosx+2cos2x，在△ABC中，角A、B、C所对的边分别为a、b、c，且满足b2+c2-a2+bc=0
（1）求角A的值；
（2）求f（A）的值；
（3）求f（B）的取值范围．
已知实数x，y满足不等式：
x-y+2≥0
1≤x≤2
y≥2
．
（1）求
y
x
的取值范围；
（2）不等式xy≤ax2+2y2恒成立，求实数a的取值范围．
在平面直角坐标系xOy中，双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的两条渐近线与抛物线y2=4x的准线相交于A，B两点．若△AOB的面积为2，则双曲线的离心率为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网