题目内容
如图,在三棱锥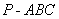 中,
中,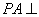 平面
平面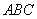 ,
, .
.
(Ⅰ)求证: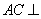
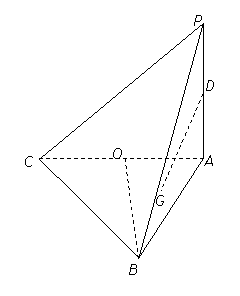
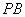 ;
;
 (Ⅱ)设
(Ⅱ)设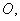
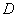 分别为
分别为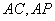 的中点,点
的中点,点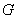 为△
为△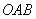 内一点,且满足
内一点,且满足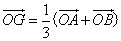 ,
,
求证: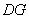 ∥面
∥面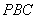 ;
;
(Ⅲ)若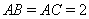 ,
,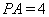 ,
,
求二面角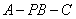 的余弦值.
的余弦值.
证明:(Ⅰ)因为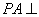 平面
平面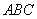 ,
, 平面
平面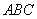 ,
,
所以 .
.
又因为 ,且
,且 ,
,
所以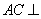 平面
平面 .
.
又因为 平面
平面 ,
,
所以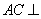
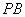 .
.
(Ⅱ)
解法1:因为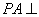 平面
平面 ,所以
,所以 ,
, .又因为
.又因为 ,
,
所以建立如图所示的空间直角坐标系 .
.
 设
设 ,
, ,
, ,
,
则 ,
, ,
, ,
,
 ,
, .
.
又因为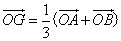 ,
,
所以 .
.
于是 ,
,
 ,
, .
.
设平面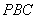 的一个法向量
的一个法向量
 ,则有
,则有
即
不妨设 ,则有
,则有 ,所以
,所以 .
.
因为 ,
,
所以 .又因为
.又因为 平面
平面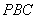 ,
,
所以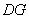 ∥平面
∥平面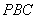 . ……………… 9分
. ……………… 9分
 |
解法2:
取 中点
中点 ,连
,连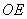 ,则
,则 .
.
由已知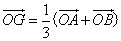 可得
可得 ,
,
则点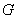 在
在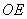 上.连结
上.连结 并延长交
并延长交 于
于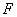 ,连
,连 .
.
因为 分别为
分别为 的中点,
的中点,
所以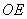 ∥
∥ ,即
,即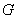 为
为 的中点.
的中点.
又因为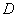 为线段
为线段 的中点,
的中点,
所以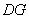 ∥
∥ .
.
 又
又 平面
平面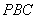 ,
, 平面
平面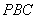 ,
,
所以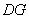 ∥平面
∥平面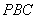 .
.
……………… 9分
(Ⅲ)由(Ⅱ)可知平面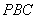 的一个法向量
的一个法向量 .
.
又因为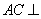 面
面 ,所以面
,所以面 的一个法向量是
的一个法向量是 .
.
又 ,
,
由图可知,二面角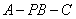 为锐角,
为锐角,
所以二面角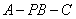 的余弦值为
的余弦值为 . ……………… 14分
. ……………… 14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 B.
B. C.
C. D.
D.


 的非空子集
的非空子集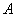 具有性质
具有性质 :当
:当 时,必有
时,必有 .则具有性质
.则具有性质



 .若
.若 ,则
,则 所有可能的取值为
所有可能的取值为 B.
B. C.
C. D.
D.


 中,
中, ,则三棱锥
,则三棱锥 —
— 的体积为
的体积为  (D)
(D)
 为不等式组
为不等式组 表示的平面区域上一点,则
表示的平面区域上一点,则 取值范围为
取值范围为 (B)
(B) (C)
(C) (D)
(D)
 的实系数一元二次方程
的实系数一元二次方程 的一个根是
的一个根是 (其中
(其中 为虚数单位),写出一个一元二次方程为 .
为虚数单位),写出一个一元二次方程为 .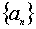 是公差为2的等差数列,若
是公差为2的等差数列,若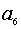 是
是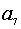 和
和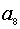 的等比中项,则
的等比中项,则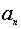 =________.
=________.