题目内容
已知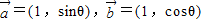 ,θ∈R;
,θ∈R;(1)若
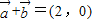 ,求sin2θ+2sinθcosθ的值;
,求sin2θ+2sinθcosθ的值;(2)若
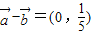 ,θ∈(π,2π),求sinθ+cosθ的值.
,θ∈(π,2π),求sinθ+cosθ的值.
【答案】分析:(1)由已知,易得出sinθ+cosθ=0,变形为tanθ=-1,将sin2θ+2sinθcosθ看作分母为1 的分式,再进行1=sin2θ+cos2θ的代换,分子分母同时除以cos2θ,
转化为关于tanθ的三角式求值
(2)考虑整体求值,先将sinθ-cosθ= 两边平方得sinθcosθ=
两边平方得sinθcosθ=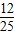 》0,判断出,∴
》0,判断出,∴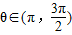 sinθ+cosθ<0,从而sinθ+cosθ=-
sinθ+cosθ<0,从而sinθ+cosθ=-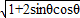 =
=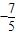 tan2θ
tan2θ
解答:解:(1)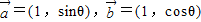 ,
,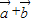 =(2,sinθ+cosθ)=(2,0)
=(2,sinθ+cosθ)=(2,0)
∴,sinθ+cosθ=0,tanθ=-1
sin2θ+2sinθcosθ=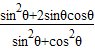 =
=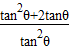 =
=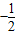
(2)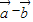 =(0,sinθ-cosθ)=
=(0,sinθ-cosθ)=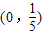 ,sinθ-cosθ=
,sinθ-cosθ= 两边平方的sinθcosθ=
两边平方的sinθcosθ=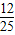
θ∈(π,2π),且sinθcosθ=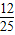 >0,∴
>0,∴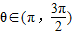 sinθ+cosθ<0
sinθ+cosθ<0
sinθ+cosθ=-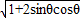 =
=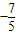
点评:本题考查三角函数式化简求值,前提牢记公式,准确应用.本题还显示了整体代换求解的特点,这也是本题的优点所在.
转化为关于tanθ的三角式求值
(2)考虑整体求值,先将sinθ-cosθ=
 两边平方得sinθcosθ=
两边平方得sinθcosθ=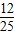 》0,判断出,∴
》0,判断出,∴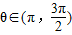 sinθ+cosθ<0,从而sinθ+cosθ=-
sinθ+cosθ<0,从而sinθ+cosθ=-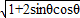 =
=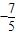 tan2θ
tan2θ解答:解:(1)
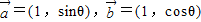 ,
,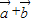 =(2,sinθ+cosθ)=(2,0)
=(2,sinθ+cosθ)=(2,0)∴,sinθ+cosθ=0,tanθ=-1
sin2θ+2sinθcosθ=
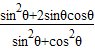 =
=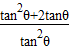 =
=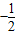
(2)
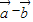 =(0,sinθ-cosθ)=
=(0,sinθ-cosθ)=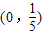 ,sinθ-cosθ=
,sinθ-cosθ= 两边平方的sinθcosθ=
两边平方的sinθcosθ=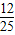
θ∈(π,2π),且sinθcosθ=
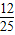 >0,∴
>0,∴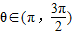 sinθ+cosθ<0
sinθ+cosθ<0sinθ+cosθ=-
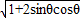 =
=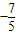
点评:本题考查三角函数式化简求值,前提牢记公式,准确应用.本题还显示了整体代换求解的特点,这也是本题的优点所在.

练习册系列答案
相关题目