题目内容
11．已知a，b，c∈R，且a＞b＞c，则下列不等式一定成立的是（ ）| A． | $\frac{1}{a}$＞$\frac{1}{b}$ | B． | 2a-b＜1 | C． | $\frac{a}{{c}^{2}+1}$＞$\frac{b}{{c}^{2}+1}$ | D． | lg（a-b）＞0 |
分析 根据对数和指数函数的性质判断B，D，举反例判断A，根据不等式的基本性质判断C．
解答 解：A、当a=-1，b=-2，显然不成立，本选项不一定成立；
B、∵a＞b，则a-b＞0．则2a-b＞1，本选项不成立；
C、由c2+1≥1，故本选项一定成立；
D、∵a-b＞0，当＜a-b＜1时，本选项不成立
故选：C
点评 此题考查了不等式的性质，利用了反例的方法，是一道基本题型．
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
1．M是△ABC所在平面内一点，$\frac{2}{3}\overrightarrow{MB}+\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow 0$，D为AC中点，则$\frac{{|\overrightarrow{MD}|}}{{|\overrightarrow{BM}|}}$的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | 1 | D． | 2 |
19．下列命题错误的是（ ）
| A． | 命题“若lgx=0，则x=0”的逆否命题为“若x≠0，则lgx≠0” | |
| B． | 若p∧q为假命题，则p，q均为假命题 | |
| C． | 命题p：?x0∈R，使得sinx0＞1，则￢p“?x∈R，均有sinx≤1 | |
| D． | “x＞2”是“$\frac{1}{x}$＜$\frac{1}{2}$”的充分不必要条件 |
6．若$\frac{1}{b}$＜$\frac{1}{a}$＜0，则下列结论不正确的是（ ）
| A． | a2＜b2 | B． | ab＞b2 | C． | a+b＜0 | D． | |a|+|b|＞a+b |
16．已知命题p：x2＞x是x＞1的充分不必要条件；命题q：若数列{an}的前n项和Sn=n2，那么数列{an}是等差数列．则下列命题是真命题的是（ ）
| A． | p∨（￢q） | B． | p∨q | C． | p∧q | D． | （￢p）∨（￢q） |
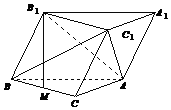如图，斜三棱柱ABC-A1B1C1的底面是直角三角形，∠ACB=90°，M是BC的中点，且BM1⊥BC，平面B1C1CB⊥平面ABC．BC=CA=AA1．
20．集合A={1，2，3，4，5}，B={x|x2-3x＜0}，则A∩B=（ ）
| A． | {1，2} | B． | {2，3} | C． | {3，4} | D． | {4，5} |