题目内容
已知函数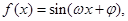 其中
其中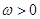 ,
,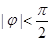
(I)若 求
求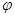 的值;
的值;
(Ⅱ)在(I)的条件下,若函数 的图像的相邻两条对称轴之间的距离等于
的图像的相邻两条对称轴之间的距离等于 ,求函数
,求函数 的解析式;并求最小正实数
的解析式;并求最小正实数 ,使得函数
,使得函数 的图像象左平移
的图像象左平移 个单位所对应的函数是偶函数。
个单位所对应的函数是偶函数。
(I)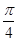 (Ⅱ)
(Ⅱ)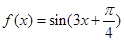 ,最小正实数
,最小正实数
解析试题分析:解法一:(I)由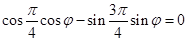 得
得 即
即 又
又
(Ⅱ)由(I)得, , 依题意,
, 依题意,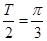
又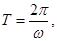 故
故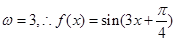
函数 的图像向左平移
的图像向左平移 个单位后所对应的函数为
个单位后所对应的函数为 
 是偶函数当且仅当
是偶函数当且仅当 , 即
, 即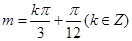 ,
,
从而,最小正实数
解法二: (I)同解法一
(Ⅱ)由(I)得,
依题意,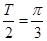 , 又
, 又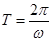 ,故
,故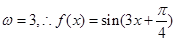
函数 的图像向左平移
的图像向左平移 个单位后所对应的函数为
个单位后所对应的函数为
 是偶函数当且仅当
是偶函数当且仅当 对
对 恒成立
恒成立
亦即 对
对 恒成立。
恒成立。

即 对
对 恒成立。
恒成立。 
故

从而,最小正实数
考点:本题考查了三角函数的性质
点评:此类问题常考查三角函数图象的变换,三角函数的定义域、值域、周期性和单调性及三角函数图象与性质的简单应用等

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
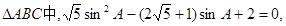 A是锐角,求
A是锐角,求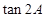 的值;
的值; 和
和 ,若它们的最小正周期的和为
,若它们的最小正周期的和为 ,且
,且 ,
, ,
, 和
和 的解析式。
的解析式。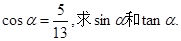
 上的函数y=f(x)的图象关于直线x=-
上的函数y=f(x)的图象关于直线x=- 对称,当x∈
对称,当x∈ 时,函数f(x)=Asin(ωx+φ)
时,函数f(x)=Asin(ωx+φ)  的图象如图所示.
的图象如图所示.
 的解.
的解.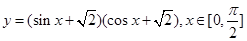 的最大值.
的最大值.  .
. ,求
,求 的最大值及此时相应的
的最大值及此时相应的 的值;
的值; 、b、c分别为角A、B、C的对边,若
、b、c分别为角A、B、C的对边,若 ,b =l,
,b =l, ,求
,求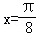 .
.
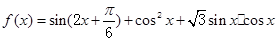 .
.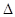 ABC的三个内角,若cosB=
ABC的三个内角,若cosB=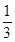 ,
,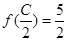 ,求sinA.
,求sinA.