题目内容
设函数f(x)=sin(2x+φ)(﹣π<φ<0),y=f(x)图象的一条对称轴是直线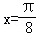 .
.
(I)求φ,并指出y=f(x)由y=sin2x作怎样变换所得.
(II)求函数y=f(x)的单调增区间;
(III)画出函数y=f(x)在区间[0,π]上的图象.
(1)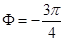 右移
右移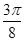 个单位 (2)
个单位 (2) (3)略
(3)略
解析试题分析:(1)因为函数f(x)=sin(2x+φ)在对称轴时有最大或最小值,据此就可得到含∅的等式,求出∅值.因为x=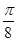 是函数y=f(x)的图象的对称轴,所以sin(2×
是函数y=f(x)的图象的对称轴,所以sin(2×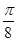 +ϕ)=±1,即
+ϕ)=±1,即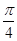 +ϕ=kπ+
+ϕ=kπ+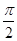 ,k∈Z.因为-π<φ<0,所以ϕ=-
,k∈Z.因为-π<φ<0,所以ϕ=-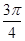 .
.
(2)借助基本正弦函数的单调性来解,因为y=sinx在区间[2kπ- 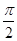 ,2kπ+
,2kπ+ 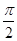 ],k∈Z上为增函数,所以只需2x-
],k∈Z上为增函数,所以只需2x-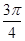 ∈[2kπ-
∈[2kπ- 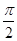 ,2kπ+
,2kπ+ 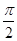 ],k∈Z,在解出x的范围
],k∈Z,在解出x的范围 即可.
即可.
(3)利用五点法作图,令x分别取0,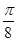 ,
,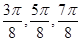 ,π,求出相应的y值,就可得到函数在区间[0,π]上的点的坐标,再把坐标表示到直角坐标系,用平滑的曲线连接即可得到所求图象。
,π,求出相应的y值,就可得到函数在区间[0,π]上的点的坐标,再把坐标表示到直角坐标系,用平滑的曲线连接即可得到所求图象。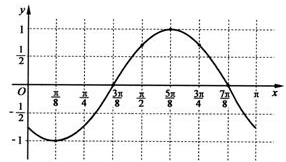
考点:三角函数的性质
点评:本小题主要考查根据三角函数的性质求解析式,以及单调区间,三角函数图象的画法,考查学生的推理和运算能力

练习册系列答案
相关题目
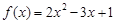 ,
, ,(
,(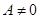 )
) ≤
≤ ≤
≤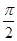 时,求
时,求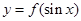 的最大值;
的最大值;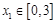 ,总存在
,总存在 ,使
,使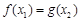 成立,求实数
成立,求实数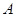 的取值范围;
的取值范围;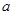 取何值时,方程
取何值时,方程 在
在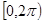 上有两解?
上有两解?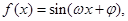 其中
其中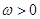 ,
,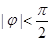
 求
求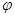 的值;
的值;  的图像的相邻两条对称轴之间的距离等于
的图像的相邻两条对称轴之间的距离等于 ,求函数
,求函数 ,使得函数
,使得函数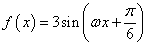 ,
,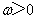 ,
,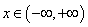 ,且以
,且以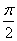 为最小正周期.
为最小正周期.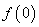 ;
;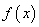 的解析式;
的解析式; ,求
,求 的值.
的值. 中,已知
中,已知 ,
,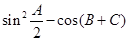 的值;
的值; ,
, ,求
,求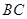 的长。
的长。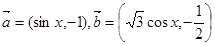 ,函数
,函数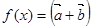 ·
·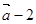
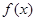 的最小正周期T及单调减区间
的最小正周期T及单调减区间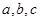 分别是△ABC内角A,B,C的对边,其中A为锐角,
分别是△ABC内角A,B,C的对边,其中A为锐角,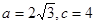 且
且 ,求A,b和△ABC的面积S
,求A,b和△ABC的面积S .
.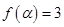 ,且
,且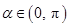 ,求
,求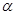 的值;
的值; 求函数
求函数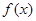 的单调递增区间;
的单调递增区间; ,不等式
,不等式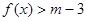 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. ,
,
 的最小正周期;
的最小正周期; 的最值.
的最值. 
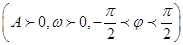 一个周期的图像如图所示。
一个周期的图像如图所示。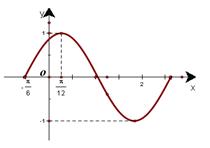
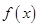 的表达式;
的表达式;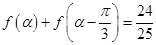 ,且
,且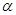 为
为 的一个内角,求
的一个内角,求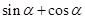 的值。
的值。