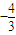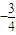Question

已知△ABC中，2sinAcosB=sinCcosB+cosCsinB．
（Ⅰ）求角B的大小；
（Ⅱ）若AB=1，向量

m

=（sinA，cos2A），

n

=（4，1），当

m

•

n

取最大值时，求△ABC的面积．

Answer 1

分析：（Ⅰ）已知等式右边利用两角和与差的正弦函数公式化简，再利用诱导公式变形，根据sinA不为0，得到cosB的值，由B为三角形的内角，利用特殊角的三角函数值即可求出B的度数；
（Ⅱ）由两向量的坐标，利用平面向量的数量积运算法则列出关系式，利用二倍角的余弦函数公式化简，整理后利用二次函数的性质，即可求出

m

•

n

的最大值，以及此时sinA的值，得到A的度数，由AB及B的度数，求出AC的长，利用三角形的面积公式即可求出三角形ABC的面积．

解答：解：（Ⅰ）∵2sinAcosB=sinCcosB+cosCsinB，
∴2sinAcosB=sin（B+C）=sin（π-A）=sinA，
∵0＜A＜π，∴sinA≠0，
∴cosB=

1

2

，
∵0＜B＜π，∴B=

π

3

；
（Ⅱ）∵

m

=（sinA，cos2A），

n

=（4，1），
∴

m

•

n

=4sinA+cos2A=4sinA+1-2sin²A=-2（sinA-1）²+3，
∴当sinA=1时，

m

•

n

取得最大值．
此时A=

π

2

（0＜A＜π），
又AB=1，B=

π

3

，∴AC=

3

，
则S_△ABC=

1

2

AB•AC=

3

2

．

点评：此题考查了两角和与差的正弦函数公式，诱导公式，平面向量的数量积运算法则，二次函数的性质，以及特殊角的三角函数值，熟练掌握公式是解本题的关键．