题目内容
若函数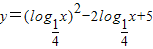 在定义域[2,4]上有最大值a,最小值b,则a-b= .
在定义域[2,4]上有最大值a,最小值b,则a-b= .
【答案】分析:由x∈[2,4],知 ,把
,把 等价转化为y=
等价转化为y= ,由此能求出最大值a和最小值b之差.
,由此能求出最大值a和最小值b之差.
解答:解:∵x∈[2,4],
∴ ,
,
∵
= ,
,
∴当 时,
时,
函数 在定义域[2,4]上最小值b=
在定义域[2,4]上最小值b= ;
;
当 时,
时,
函数 在定义域[2,4]上有最大值a=8,
在定义域[2,4]上有最大值a=8,
∴a-b=8- .
.
故答案为: .
.
点评:本题考查对数函数的性质和应用,解题时要认真审题,注意二次函数的性质的合理运用.
 ,把
,把 等价转化为y=
等价转化为y= ,由此能求出最大值a和最小值b之差.
,由此能求出最大值a和最小值b之差.解答:解:∵x∈[2,4],
∴
 ,
,∵

=
 ,
,∴当
 时,
时,函数
 在定义域[2,4]上最小值b=
在定义域[2,4]上最小值b= ;
;当
 时,
时,函数
 在定义域[2,4]上有最大值a=8,
在定义域[2,4]上有最大值a=8,∴a-b=8-
 .
.故答案为:
 .
.点评:本题考查对数函数的性质和应用,解题时要认真审题,注意二次函数的性质的合理运用.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
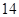 分)
分)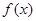 在定义域
在定义域 内某区间
内某区间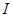 上是增函数,而
上是增函数,而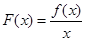 在
在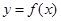 在
在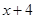 ,
,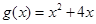 在
在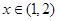 是否是“弱增函数”,
是否是“弱增函数”,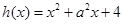 (
(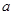 是常数且
是常数且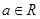 )在
)在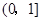 上是“弱增函数”.
上是“弱增函数”.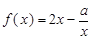 的定义域为
的定义域为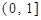 (
(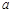 为实数).
为实数).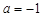 时,求函数
时,求函数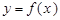 的值域;
的值域;
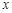 的值.
的值. 在定义域[2,4]上有最大值a,最小值b,则a-b=________.
在定义域[2,4]上有最大值a,最小值b,则a-b=________.