题目内容
设f(x)=ax2+bx,若1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围.
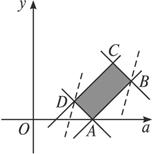
解:由已知可得![]() 该不等式组的可行域是一个长方形ABCD,其中A(2,0),B(3,1),C(
该不等式组的可行域是一个长方形ABCD,其中A(2,0),B(3,1),C(![]() ,
,![]() ),D(
),D(![]() ,
,![]() ),f(-2)=4a-2b经过B时取得最大值10,经过D时有最小值5.
),f(-2)=4a-2b经过B时取得最大值10,经过D时有最小值5.
∴f(-2)的取值范围是[5,10].

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
题目内容
设f(x)=ax2+bx,若1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围.
解:由已知可得![]() 该不等式组的可行域是一个长方形ABCD,其中A(2,0),B(3,1),C(
该不等式组的可行域是一个长方形ABCD,其中A(2,0),B(3,1),C(![]() ,
,![]() ),D(
),D(![]() ,
,![]() ),f(-2)=4a-2b经过B时取得最大值10,经过D时有最小值5.
),f(-2)=4a-2b经过B时取得最大值10,经过D时有最小值5.

∴f(-2)的取值范围是[5,10].

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案