题目内容
12.已知点M为圆C1:(x+2)2+(y-2$\sqrt{5}$)2=1上的任意一点,点N为动圆C2:x2+y2-4ax-2(a+1)y+5a2+2a=0(a∈R)的圆心,则线段MN的最小值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 2$\sqrt{5}$ |
分析 求出圆的标准方程,求出圆心坐标和半径,利用数形结合进行求解即可.
解答 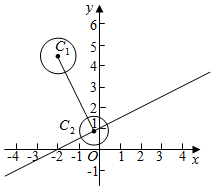 解:圆C1:(x+2)2+(y-2$\sqrt{5}$)2=1的圆心坐标为(-2,2$\sqrt{5}$),半径R=1,
解:圆C1:(x+2)2+(y-2$\sqrt{5}$)2=1的圆心坐标为(-2,2$\sqrt{5}$),半径R=1,
动圆C2:x2+y2-4ax-2(a+1)y+5a2+2a=0的标准方程为(x-2a)2+(y-a-1)2=1
则圆心坐标为C2:(2a,a+1),半径r=1,C2:(2a,a+1)在直线l:y=$\frac{1}{2}$x+1,
则C1C2⊥l时,线段|C1C2|最小,此时MN最小,
此时|C1C2|=$\frac{|\frac{1}{2}×(-2)-2\sqrt{5}+1|}{\sqrt{(\frac{1}{2})^{2}+1}}$=$\frac{2\sqrt{5}}{\sqrt{\frac{5}{4}}}=\frac{2\sqrt{5}}{\frac{\sqrt{5}}{2}}$=4,
此时MN的最小值为|C1C2|-R=4-1=3,
故选:C.
点评 本题主要考查与圆的位置关系的应用,利用数形结合转化为点到直线的距离是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.设直角坐标平面内与两个定点A(-2,0),B(2,0)的距离之差的绝对值等于2的点的轨迹是E,C是轨迹E上一点,直线BC垂直于x轴,则$\overrightarrow{AC}$$•\overrightarrow{BC}$=( )
| A. | -9 | B. | -3 | C. | 3 | D. | 9 |
1.若复数z=(3+bi)(1+i)-2是纯虚数(b∈R),则|z|=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
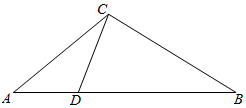 如图,在△ABC中,点D在边AB上,AC=7,CD=5,BC=$\sqrt{31}$,BD=2AD
如图,在△ABC中,点D在边AB上,AC=7,CD=5,BC=$\sqrt{31}$,BD=2AD