题目内容
(本小题满分14分)给定正奇数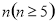 ,数列
,数列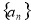 :
: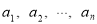 是1,2,…,
是1,2,…,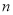 的一个排列,定义E(
的一个排列,定义E(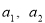 ,…,
,…,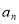 )
)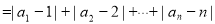 为数列
为数列 :
: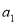 ,
, ,…,
,…,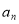 的位差和.
的位差和.
(1)当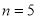 时,求数列
时,求数列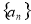 :1,3,4,2,5的位差和;
:1,3,4,2,5的位差和;
(2)若位差和E(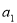 ,
,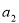 ,…,
,…,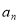 )=4,求满足条件的数列
)=4,求满足条件的数列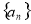 :
: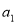 ,
,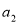 ,…,
,…,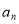 的个数;
的个数;
(3)若位差和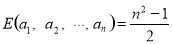 ,求满足条件的数列
,求满足条件的数列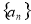 :
: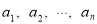 的个数.
的个数.
(1)4;(2) ;(3)
;(3) .
.
【解析】
试题分析:(1)根据定义直接计算即可;(2)当位差和为4时,分两情况:当 ,
, ,
, ,
, ,且
,且 ,可算得共有
,可算得共有 种情况,
种情况, 分别等于
分别等于 ,
, ,
, 或
或 ,
, ,
, 或
或 ,
, ,其他项
,其他项 (其中
(其中 )时,有
)时,有 种可能,两种情况相加即可;(3)将
种可能,两种情况相加即可;(3)将 去绝对值符号后,所得结果为
去绝对值符号后,所得结果为
 1
1 1
1 2
2 2
2 3
3 3
3 …
…


 的形式,其中恰好有
的形式,其中恰好有 个数前面为减号,这表明
个数前面为减号,这表明


 ,
,
此不等式成立是因为前面为减号的 个数最小为:2个1,2个2,…,2个
个数最小为:2个1,2个2,…,2个 和1个
和1个 .
.
上面的讨论表明,题中所求的数列 是使得E(
是使得E( )最大的数列,这样的数列在
)最大的数列,这样的数列在 时,要求从1,2,…,
时,要求从1,2,…, 中任选一个数作为
中任选一个数作为 ,将剩余数中较大的
,将剩余数中较大的 个数的排列作为
个数的排列作为 …,
…, 的对应值,较小的
的对应值,较小的 个数的排列作为
个数的排列作为 ,
, ,…,
,…, 的对应值,于是所求数列的个数为
的对应值,于是所求数列的个数为 .满足条件的数列的个数为
.满足条件的数列的个数为
试题解析:(1)E(1,3,4,2,5)=|1-1|+|3-2|+|4-3|+|2-4|+|5-5|=4;(3分)
(2)若数列 :
: ,
, ,…,
,…, 的位差和E(
的位差和E( ,
, ,…,
,…, )=4,有如下两种情况:
)=4,有如下两种情况:
情况一:当 ,
, ,
, ,
, ,且
,且 ,其他项
,其他项 (其中
(其中 )时,有
)时,有 种可能;(5分)
种可能;(5分)
情况二:当 分别等于
分别等于 ,
, ,
, 或
或 ,
, ,
, 或
或 ,
, ,其他项
,其他项 (其中
(其中 )时,有
)时,有 种可能;(7分)
种可能;(7分)
综上,满足条件的数列 :
: 的个数为
的个数为
 .(8分)
.(8分)
例如: 时,
时,
情况一:形如2,1,4,3,5,共有2+1=3种:2,1,4,3,5;2,1,3,5,4;1,3,2,5,4;
情况二:形如3,2,1,4,5,共有5-2=3种:3,2,1,4,5;1,4,3,2,5;1,2,5,4,3;
形如2,3,1,4,5,共有5-2=3种:2,3,1,4,5;1,3,4,2,5;1,2,4,5,3;
形如3,1,2,4,5,共有5-2=3种:3,1,2,4,5;1,4,2,3,5;1,2,5,3,4.
(3)将 去绝对值符号后,所得结果为
去绝对值符号后,所得结果为
 1
1 1
1 2
2 2
2 3
3 3
3 …
…



的形式,其中恰好有 个数前面为减号,这表明
个数前面为减号,这表明


 ,(10分)
,(10分)
此不等式成立是因为前面为减号的 个数最小为:2个1,2个2,…,2个
个数最小为:2个1,2个2,…,2个 和1个
和1个 .(11分)
.(11分)
上面的讨论表明,题中所求的数列 是使得E(
是使得E( )最大的数列,这样的数列在
)最大的数列,这样的数列在 时,要求从1,2,…,
时,要求从1,2,…, 中任选一个数作为
中任选一个数作为 ,将剩余数中较大的
,将剩余数中较大的 个数的排列作为
个数的排列作为 …,
…, 的对应值,较小的
的对应值,较小的 个数的排列作为
个数的排列作为 ,
, ,…,
,…, 的对应值,于是所求数列的个数为
的对应值,于是所求数列的个数为 .
.
综上,满足条件的数列的个数为 (14分)
(14分)
例如: 时,
时,
E( )
) .
.





此不等式成立是因为前面为减号的5个数最小为:2个1,2个2和1个3.
若E( )=12,
)=12, ,此时
,此时 时,要求从1,2,3,4,5中任选一个数作为
时,要求从1,2,3,4,5中任选一个数作为 ,将剩余数中较大的2个数的排列作为
,将剩余数中较大的2个数的排列作为 ,
, 的对应值,较小的2个数的排列作为
的对应值,较小的2个数的排列作为 的对应值,于是所求数列的个数为
的对应值,于是所求数列的个数为 .
.
4,5,1,2,3;4,5,1,3,2;5,4,1,2,3;5,4,1,3,2;
4,5,2,1,3;4,5,2,3,1;5,4,2,1,3;5,4,2,3,1;
4,5,3,1,2;4,5,3,2,1;5,4,3,1,2;5,4,3,2,1;
3,5,4,1,2;3,5,4,2,1;5,3,4,1,2;5,3,4,2,1;
3,4,5,1,2;3,4,5,2,1;4,3,5,1,2;4,3,5,2,1.
题目背景:假设现在有 种物品,已经按照某种标准排列,并依次确定编号为1,2,…,
种物品,已经按照某种标准排列,并依次确定编号为1,2,…, ,鉴别师事先不知道物品的标准排列编号,而是根据自己的判断,对这
,鉴别师事先不知道物品的标准排列编号,而是根据自己的判断,对这 种物品进行排列依次编号为
种物品进行排列依次编号为 ,其中
,其中 是1,2,…,
是1,2,…, 的一个排列,那么可以用数列
的一个排列,那么可以用数列 :
: 的位差和
的位差和
E( )=
)= ,
,
来评判鉴别师的能力.
当E( )越小,说明鉴别师能力越强;反之越大,说明鉴别师能力越弱;
)越小,说明鉴别师能力越强;反之越大,说明鉴别师能力越弱;
当E( )=0,说明鉴别师给出的排列编号与标准排列编号一致,判断完全正确;
)=0,说明鉴别师给出的排列编号与标准排列编号一致,判断完全正确;
第二问,位差和E( )=4时,给出数列
)=4时,给出数列 :
: 的情况;
的情况;
第三问,说明位差和E( )最大值为
)最大值为 ,且给出取得最大值时,数列
,且给出取得最大值时,数列 :
: 的情况.
的情况.
考点:新定义问题、数列求和、基本不等式、排列与组合.

 阅读快车系列答案
阅读快车系列答案 轴截得的弦长等于( )
轴截得的弦长等于( ) (D)1
(D)1 是等差数列
是等差数列 的前n项和,且
的前n项和,且 成等比数列,则
成等比数列,则 等于( )
等于( ) 被圆
被圆 截得的弦长为__________.
截得的弦长为__________.
 B.
B.  C.
C.  D.
D. 
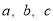 ,满足
,满足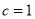 ,且
,且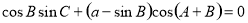 .
.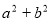 的最大值,并求取得最大值时角A,B的值.
的最大值,并求取得最大值时角A,B的值. 不等式
不等式 在
在 上恒成立,则实数
上恒成立,则实数 的取值范围是
的取值范围是 B.
B.  C.
C.  D.
D. 
 满足
满足 ,则
,则 的最小值为 .
的最小值为 . 是等差数列,若
是等差数列,若 ,则
,则 的值是 .
的值是 .