题目内容
已知直线y=kx-1与双曲线x2-y2=1的左支交于A、B两点,若另有一条直线l经过P(-2,0)及线段AB的中点Q.(1)求k的取值范围;
(2)求直线l在y轴上的截距b的取值范围.
解：(1)把y=kx-1代入双曲线方程x2-y2=1,?
化简整理得(1-k2)x2+2kx-2=0.?
由题设条件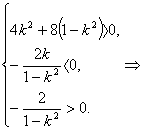
.?
(2)设A(x1,y1)、B(x2,y2)、Q(x,y),则x=
=
, y=
,
∴直线l的方程为y=
(x+2).?
令x=0,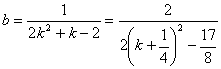
,?
∵-
,u=2k2+k-2为减函数,?
∴
.又u≠0,∴b＜-2或b＞2+
.
点评：注意正确转化直线与双曲线的单支相交后的不等式组.
练习册系列答案
世纪百通期末金卷系列答案
相关题目
（理）已知直线y=kx+1（k∈R）与椭圆
+
=1总有交点，则m的取值范围为（ ）
| x2 |
| 2 |
| y2 |
| m |
| A、（1，2] |
| B、[1，2） |
| C、[1，2）∪[2，+∞） |
| D、（2，+∞） |