题目内容
在△ABC中，cos（A+
）=
，则cos2A= ．
| π |
| 4 |
| 3 |
| 5 |
考点：两角和与差的余弦函数
专题：三角函数的求值
分析：根据余弦函数的倍角公式，以及三角函数的诱导公式将条件进行化简，即可得到结论．
解答：
解：cos2A=sin（2A+
）=2sin（A+
）cos（A+
），
在△ABC中，cos（A+
）=
＞0，
∴0＜A+
＜
，
∴sin（A+
）=
，
∴cos2A=sin2（A+
）=2sin（A+
）cos（A+
）=2×
×
=
，
故答案为：
．
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
在△ABC中，cos（A+
| π |
| 4 |
| 3 |
| 5 |
∴0＜A+
| π |
| 4 |
| π |
| 2 |
∴sin（A+
| π |
| 4 |
| 4 |
| 5 |
∴cos2A=sin2（A+
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3 |
| 5 |
| 4 |
| 5 |
| 24 |
| 25 |
故答案为：
| 24 |
| 25 |
点评：本题主要考查三角函数的求值，利用诱导公式以及三角函数的倍角公式是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
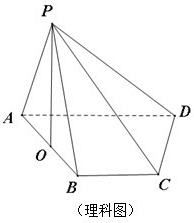（理科做）如图，四棱锥P-ABCD的底面ABCD是直角梯形，∠ABC=90°，BC∥AD，且AB=AD=2BC，顶点P在底面ABCD内的射影恰好落在AB的中点O上．
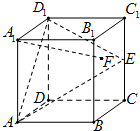在正方体ABCD-A1B1C1D1中，E是棱CC1的中点，F是侧面BCC1B1内的动点，且A1F∥平面D1AE，则A1F与平面BCC1B1所成角的正切值的取值范围是已知命题p：-4＜x-a＜4，命题q：（x-1）（x-3）＜0，且q是p的充分而不必要条件，则a的取值范围是（ ）
| A、[-1，5] |
| B、[-1，5） |
| C、（-1，5] |
| D、（-1，5） |