题目内容
设向量 =(1,2m),
=(1,2m), =(m+1,1),
=(m+1,1), =(2,m),若(
=(2,m),若( +
+ )⊥
)⊥ ,则|
,则| |=________.
|=________.

分析:由
 =(1,2m),
=(1,2m), =(m+1,1),
=(m+1,1), =(2,m),知
=(2,m),知 =(3,3m),由(
=(3,3m),由( +
+ )⊥
)⊥ ,知(
,知( )
)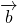 =3(m+1)+3m=0,由此能求出|
=3(m+1)+3m=0,由此能求出| .
.解答:∵
 =(1,2m),
=(1,2m), =(m+1,1),
=(m+1,1), =(2,m),
=(2,m),∴
 =(3,3m),
=(3,3m),∵(
 +
+ )⊥
)⊥ ,
,∴(
 )
)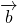 =3(m+1)+3m=0,
=3(m+1)+3m=0,∴m=-
 ,即
,即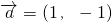
∴
 =
= .
.故答案为:
 .
.点评:本题考查数量积判断两个平面向量的垂直关系的应用,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目