题目内容
【题目】在四棱锥
中，
，
，
，
为棱
上一点（不包括端点），且满足
.
（1）求证：平面
平面
；
（2）
为
的中点，求二面角
的余弦值的大小.
【答案】（1）证明见解析；（2）
.
【解析】
（1）根据传递性，由
平面
，得到平面
平面
（2）作
于点
，过点作
，建立空间直角坐标系，求出各平面法向量后根据夹角公式求得二面角余弦值
（1）证明：因为
，
，所以
，
又
，
，所以平面，
又
平面，所以平面平面.
（2） 
如图，作于点，过点作，
则
，
，
两两垂直，故以为坐标原点，
直线，，分别为
轴、
轴、
轴建立如图所示空间直角坐标系.
设
，则
，
，
，所以
，
又
，所以
，
，
，
所以
，
，
，
，
.
因为
为
的中点，所以
.
，
，
令
为平面
的法向量，
则有
即
不妨设
，则
.
易知平面
的一个法向量为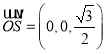
，
.
因为二角
为钝角，
所以二面角的余弦值为.
练习册系列答案
相关题目
【题目】小明在10场篮球比赛中的投篮情况统计如下（假设各场比赛相互独立）：
场次 | 投篮次数 | 命中次数 |
主场1 | 22 | 12 |
主场2 | 15 | 12 |
主场3 | 12 | 8 |
主场4 | 23 | 8 |
主场5 | 24 | 20 |
场次 | 投篮次数 | 命中次数 |
客场1 | 18 | 8 |
客场2 | 13 | 12 |
客场3 | 21 | 7 |
客场4 | 18 | 15 |
客场5 | 25 | 12 |
（1）从上述比赛中随机选择一场，求小明在该场比赛中投篮命中率超过0.6的概率；
（2）从上述比赛中随机选择一个主场和一个客场，求小明的投篮命中率一场超过0.6，一场不超过0.6的概率.
