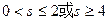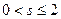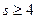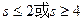题目内容
已知点M(x, y)在不等式组 所表示的平面区域内,则
所表示的平面区域内,则
 的值域为
的值域为
 所表示的平面区域内,则
所表示的平面区域内,则 的值域为
的值域为A. | B. |
C. | D. |
B
分析:先根据约束条件画出可行域,再利用几何意义求最值,r=(x-1)2+(y-2)2表示动点到点P(1,2)的距离的平方,只需求出可行域内的动点到P点的距离最大最小值即可.

解:注意到目标函数所表示的几何意义是动点到P(1,2)的距离的平方,作出可行域.
易知当Q点在A点时取得目标函数的最大值,
可知A点的坐标为(-3,1),
代入目标函数中,可得zmax=42+12=17.
当Q点在B点时取得目标函数的最小值,
可知B点的坐标为(1,0),
代入目标函数中,可得zmax=22+22=8.
故选B.

练习册系列答案
相关题目
 满足不等式组
满足不等式组 目标函数
目标函数 的最大值为2,则实数
的最大值为2,则实数 的值是
的值是
 满足
满足 ,若不等式
,若不等式 恒成立,求
恒成立,求 最大值
最大值 ,向区域
,向区域 内随机投一点P,点P落在区域M内的概率为
内随机投一点P,点P落在区域M内的概率为



 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最大值为( )
的最大值为( )  2
2  3
3  4
4  5
5 满足约束条件,
满足约束条件, 则
则 的最小值是( )
的最小值是( ) B.
B. C.
C. D.
D.
 则
则 的最大值为________.
的最大值为________.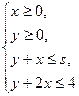 表示的平面区域是一个三角形,则实数s的取值范围是( )
表示的平面区域是一个三角形,则实数s的取值范围是( )