Question

已知双曲线

x2

a2

-

y2

b2

=1(a＞0，b＞0)的离心率为e，右顶点为A，左、右焦点分别为F₁、F₂，点E为右准线上的动点，∠AEF₂的最大值为θ．
（1）若双曲线的左焦点为F₁（-4，0），一条渐近线的方程为3x-2y=0，求双曲线的方程；
（2）求sinθ（用e表示）；
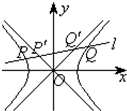
（3）如图，如果直线l与双曲线的交点为P、Q，与两条渐近线的交点为P'、Q'，O为坐标原点，求证：

OP

+

OQ

=

OP′

+

OQ′

．

Answer 1

分析：（1）方法1：设双曲线的方程为

x2

a2

-

y2

16-a2

=1，其渐近线的方程为y=±

16-a2

a

x．因为一条渐近线的方程是y=

3

2

x，所以

16-a2

a

=

3

2

，由此能求出双曲线的方程．
方法2：双曲线的一条渐近线是3x-2y=0，设双曲线的方程为

x2

4

-

y2

9

=λ．由焦点是（-4，0），得4λ+9λ=16，由此能求出双曲线的方程．
（2）设经过点A、F₂的圆C与准线相切于点M，交EF₂于点N．由∠AMF₂=∠ANF₂≥∠AEF₂，知∠AMF₂=θ．由A（a，0），F₂（c，0），知C(

a+c

2

，y0)，由此能求出sinθ（用e表示）．
（3）方法1：当直线l的斜率存在时，设直线l的方程为y=mx+n，代入

x2

a2

-

y2

b2

=1中得（b²-a²m²）x²-2a²mnx-a²（n²+b²）=0．设P（x₁，y₁），Q（x₂，y₂），线段PQ的中点为G（α，β），则α=

x1+x2

2

=

a2mn

b2-a2m2

．由此能证明

OP

+

OQ

=

OP′

+

OQ′

．
方法2：当直线l的斜率不存在或为零时，即直线l垂直于x轴或垂直于y轴时，由对称性可知线段PQ与线段P'Q'有共同的中点，所以|PP'|=|QQ'|．设l：y=kx+m（k≠0）．设PQ的中点为G（x₀，y₀），P'Q'的中点为G'（x'₀，y'₀），则由点差法可得

x0

a2

=

y0

b2

k，且

x′0

a2

=

y′0

b2

k，由此能够证明

OP

+

OQ

=

OP′

+

OQ′

．

解答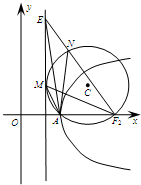：解：（1）方法1 
 双曲线的左焦点为F₁（-4，0），
设双曲线的方程为

x2

a2

-

y2

16-a2

=1，
则其渐近线的方程为

x2

a2

-

y2

16-a2

=0，即y=±

16-a2

a

x．
又∵一条渐近线的方程是y=

3

2

x，
∴

16-a2

a

=

3

2

，得a2=

64

13

，16-a2=

144

13

．
故双曲线的方程为

13x2

64

-

13y2

144

=1．
方法2
∵双曲线的一条渐近线是3x-2y=0，即

x

2

-

y

3

=0，
∴可设双曲线的方程为

x2

4

-

y2

9

=λ．
∵焦点是（-4，0），
∴由

x2

4λ

-

y2

9λ

=1得4λ+9λ=16，
∴λ=

16

13

，
∴双曲线的方程为

13x2

64

-

13y2

144

=1．
（2）设经过点A、F₂的圆C与准线相切于点M，交EF₂于点N．
∵∠AMF₂=∠ANF₂≥∠AEF₂（当E与M重合时取“=”），
∴∠AMF₂=θ．
∵A（a，0），F₂（c，0），
∴C(

a+c

2

，y0)，
又∵M(

a2

c

，y0)，
∴圆C的半径R=|CM|=

a+c

2

-

a2

c

．
由正弦定理得

|AF2|

sinθ

=2R，
∴sinθ=

|AF2|

2R

=

c-a

a+c- 2a2 c

=

c(a-c)

(2a+c)(a-c)

=

c

2a+c

=

c a

2+ c a

=

e

e+2

．
（3）证明：方法1 
 当直线l的斜率存在时，设直线l的方程为y=mx+n，
代入

x2

a2

-

y2

b2

=1中得（b²-a²m²）x²-2a²mnx-a²（n²+b²）=0．
设P（x₁，y₁），Q（x₂，y₂），线段PQ的中点为G（α，β），
则α=

x1+x2

2

=

a2mn

b2-a2m2

．
同理，将y=mx+n代入渐近线方程

x2

a2

-

y2

b2

=0中，
得（b²-a²m²）x²-2a²mnx-a²n²=0．
设P'（x'₁，y'₁），Q'（x'₂，y'₂），
线段P'Q'的中点为G'（α'，β'），
则α′=

x′1+x′2

2

=

a2mn

b2-a2m2

，
∴α=α'，即线段PQ与线段P'Q'有共同的中点．
当直线l的斜率不存在时，即直线l垂直于x轴时，
由对称性可知线段PQ与线段P'Q'有共同的中点
．∴

OP + OQ

2

=

OP′ + OQ′

2

，即

OP

+

OQ

=

OP′

+

OQ′

．
方法2  
当直线l的斜率不存在或为零时，
即直线l垂直于x轴或垂直于y轴时，
由对称性可知线段PQ与线段P'Q'有共同的中点，
∴|PP'|=|QQ'|．
当直线l的斜率存在且不为零时，可设l：y=kx+m（k≠0）．
设PQ的中点为G（x₀，y₀），P'Q'的中点为G'（x'₀，y'₀），
则由点差法可得

x0

a2

=

y0

b2

k，
且

x′0

a2

=

y′0

b2

k，
∴点G、G'在直线l'：

x

a2

=

y

b2

k，
即y=

b2

a2k

x上．
又∵点G、G'在直线l：y=kx+m上，
∴点G、G'同为直线l与l'的交点．
故点G、G'重合，
∴

OP + OQ

2

=

OP′ + OQ′

2

，
即

OP

+

OQ

=

OP′

+

OQ′

．

点评：通过几何量的转化考查用待定系数法求曲线方程的能力，通过直线与圆锥曲线的位置关系处理，考查学生的运算能力．通过向量与几何问题的综合，考查学生分析转化问题的能力，探究研究问题的能力，并体现了合理消元，设而不解的代数变形的思想．对数学思维的要求比较高，有一定的探索性．综合性强，难度大，易出错．