题目内容
已知fn(x)=a1x+a2x2+…+anxn,fn(-1)=(-1)n•n(n∈N*).
(Ⅰ)求a1、a2、a3;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)令bn=fn(
),判断数列{bn}的单调性,并且证明.
(Ⅰ)求a1、a2、a3;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)令bn=fn(
| 1 |
| 3 |
考点:等差数列的通项公式,数列的函数特性
专题:等差数列与等比数列
分析:(I)由已知条件,利用递推思想能够依资次求出a1、a2、a3的值.
(II)由题意知(-1)n+1an+1=fn+1(-1)-fn(-1)=(-1)n+1•(n+1)-(-1)n•n,由此能求出an=2n-1.
(III)由fn(x)=x+3x2+5x3+…+(2n-1)xn,利用错位相减法能证明fn(
)是单调增数列.
(II)由题意知(-1)n+1an+1=fn+1(-1)-fn(-1)=(-1)n+1•(n+1)-(-1)n•n,由此能求出an=2n-1.
(III)由fn(x)=x+3x2+5x3+…+(2n-1)xn,利用错位相减法能证明fn(
| 1 |
| 3 |
解答:
解:(I)∵fn(x)=a1x+a2x2+…+anxn,fn(-1)=(-1)n•n(n∈N*).
∴f1(-1)=-a1=-1,解得a1=1,(1分)
f2(-1)=-a1+a2=2,解得a2=3,
f3(-1)=-a1+a2-a3=-3,解得a3=5.(3分)
(II)∵fn(x)=a1x+a2x2+…+anxn,
fn(-1)=(-1)n•n(n∈N*).
∴(-1)n+1an+1=fn+1(-1)-fn(-1)
=(-1)n+1•(n+1)-(-1)n•n,
∴an+1=(n+1)+n,
即an+1=2n+1(n≥1)
当n=1时,a1=1
所以对于任意的n=1,2,3…,an=2n-1.(8分)
(III)数列{bn},证明如下:
∵fn(x)=x+3x2+5x3+…+(2n-1)xn,
∴fn(
)=
+3(
)2+5(
)3+…+(2n-1)(
)n①
fn+1(
)-fn(
)=(2n+1)(
)n+1>0,
∴数列{bn}是单调增数列.(12分).
∴f1(-1)=-a1=-1,解得a1=1,(1分)
f2(-1)=-a1+a2=2,解得a2=3,
f3(-1)=-a1+a2-a3=-3,解得a3=5.(3分)
(II)∵fn(x)=a1x+a2x2+…+anxn,
fn(-1)=(-1)n•n(n∈N*).
∴(-1)n+1an+1=fn+1(-1)-fn(-1)
=(-1)n+1•(n+1)-(-1)n•n,
∴an+1=(n+1)+n,
即an+1=2n+1(n≥1)
当n=1时,a1=1
所以对于任意的n=1,2,3…,an=2n-1.(8分)
(III)数列{bn},证明如下:
∵fn(x)=x+3x2+5x3+…+(2n-1)xn,
∴fn(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
fn+1(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴数列{bn}是单调增数列.(12分).
点评:本题考查数列的通项公式的求法,考查数列的单调性的判断并证明,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
不等式x2+2x-3≤0的解是( )
| A、(-∞,-3] |
| B、[1,+∞) |
| C、[-3,1] |
| D、(-∞,-3]∪[1,+∞) |
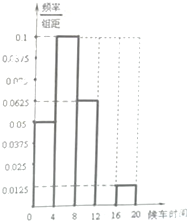 常州公交公司为了调整302线路发车的时间间隔,在某站点对乘客进行了候车时间的调查,以下是候车时间的频率分布表和频率分布直方图.
常州公交公司为了调整302线路发车的时间间隔,在某站点对乘客进行了候车时间的调查,以下是候车时间的频率分布表和频率分布直方图.