题目内容
函数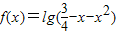 ,则f(x)的单调递减区间是 .
,则f(x)的单调递减区间是 .
【答案】分析:由 -x-x2>0求出函数的定义域,再由二次函数和对数函数的单调性,以及“同增异减”法则求出原函数的减区间.
-x-x2>0求出函数的定义域,再由二次函数和对数函数的单调性,以及“同增异减”法则求出原函数的减区间.
解答:解:由题意知, -x-x2>0,即4x2+4x-3<0,解得
-x-x2>0,即4x2+4x-3<0,解得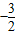 <x<
<x< ,故函数的定义域是(
,故函数的定义域是(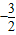 ,
, ),
),
令y=-x2-x+ =-
=-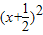 +1,则函数y在(
+1,则函数y在(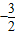 ,-
,- )上是增函数,在(-
)上是增函数,在(- ,
, )上是减函数,
)上是减函数,
又∵y=lgx在定义域上是增函数,
∴f(x)的单调递减区间是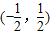 .
.
故答案为: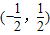 .
.
点评:本题的考点是对数型复合函数的单调性,根据真数大于零求出函数的定义域,这是易出错的地方,再由“同增异减”判断原函数的单调性.
 -x-x2>0求出函数的定义域,再由二次函数和对数函数的单调性,以及“同增异减”法则求出原函数的减区间.
-x-x2>0求出函数的定义域,再由二次函数和对数函数的单调性,以及“同增异减”法则求出原函数的减区间.解答:解:由题意知,
 -x-x2>0,即4x2+4x-3<0,解得
-x-x2>0,即4x2+4x-3<0,解得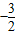 <x<
<x< ,故函数的定义域是(
,故函数的定义域是(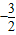 ,
, ),
),令y=-x2-x+
 =-
=-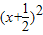 +1,则函数y在(
+1,则函数y在(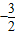 ,-
,- )上是增函数,在(-
)上是增函数,在(- ,
, )上是减函数,
)上是减函数,又∵y=lgx在定义域上是增函数,
∴f(x)的单调递减区间是
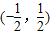 .
.故答案为:
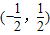 .
.点评:本题的考点是对数型复合函数的单调性,根据真数大于零求出函数的定义域,这是易出错的地方,再由“同增异减”判断原函数的单调性.

练习册系列答案
相关题目
 ,则f(x)的单调减区间是________.
,则f(x)的单调减区间是________. ,则f(x)的单调减区间是 .
,则f(x)的单调减区间是 .