题目内容
中心在坐标原点,焦点在x轴上的椭圆,它的离心率为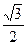 ,与直线x+y-1=0相交于两点M、N,且以
,与直线x+y-1=0相交于两点M、N,且以 为直径的圆经过坐标原点.求椭圆的方程.
为直径的圆经过坐标原点.求椭圆的方程.
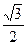 ,与直线x+y-1=0相交于两点M、N,且以
,与直线x+y-1=0相交于两点M、N,且以 为直径的圆经过坐标原点.求椭圆的方程.
为直径的圆经过坐标原点.求椭圆的方程.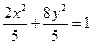
由题意,设中心在坐标原点,焦点在x轴上的椭圆方程为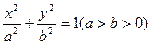 ,
,
∵离心率e=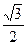 ∴a=2b,∴椭圆的方程可化为
∴a=2b,∴椭圆的方程可化为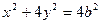
设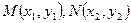 ,由于点M、N都在直线x+y-1=0上,
,由于点M、N都在直线x+y-1=0上,
因此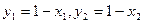 ,
,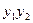 =
=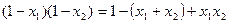
∵以 为直径的圆经过坐标原点,即OM⊥ON,∴
为直径的圆经过坐标原点,即OM⊥ON,∴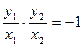 即
即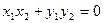 ,
,
即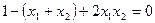 ,将直线x+y-1=0与椭圆的方程
,将直线x+y-1=0与椭圆的方程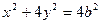 联立消去y得:
联立消去y得:
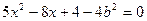 ,∵M、N是直线与椭圆的两交点,
,∵M、N是直线与椭圆的两交点,
∴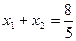 ,
,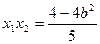 ,代入
,代入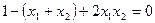 得:
得:
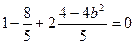 , 解得
, 解得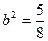 ,∴
,∴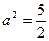 ,
,
∴所求的椭圆方程为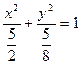 ,即
,即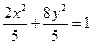 .
.
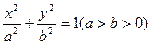 ,
,∵离心率e=
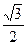 ∴a=2b,∴椭圆的方程可化为
∴a=2b,∴椭圆的方程可化为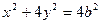
设
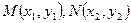 ,由于点M、N都在直线x+y-1=0上,
,由于点M、N都在直线x+y-1=0上,因此
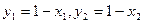 ,
,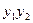 =
=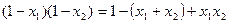
∵以
 为直径的圆经过坐标原点,即OM⊥ON,∴
为直径的圆经过坐标原点,即OM⊥ON,∴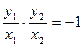 即
即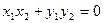 ,
,即
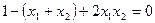 ,将直线x+y-1=0与椭圆的方程
,将直线x+y-1=0与椭圆的方程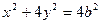 联立消去y得:
联立消去y得: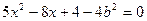 ,∵M、N是直线与椭圆的两交点,
,∵M、N是直线与椭圆的两交点,∴
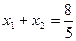 ,
,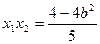 ,代入
,代入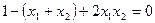 得:
得: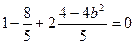 , 解得
, 解得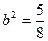 ,∴
,∴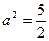 ,
,∴所求的椭圆方程为
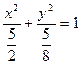 ,即
,即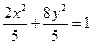 .
.
练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
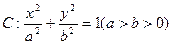 的离心率为
的离心率为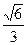 ,F为椭圆在x轴正半轴上的焦点,M、N两点在椭圆C上,且
,F为椭圆在x轴正半轴上的焦点,M、N两点在椭圆C上,且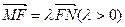 ,定点A(-4,0).
,定点A(-4,0).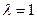 时.,
时.,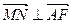 ;
;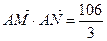 ,求椭圆C的方程;
,求椭圆C的方程;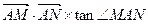 的值为6
的值为6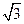 时, 求出直线MN的方程.
时, 求出直线MN的方程.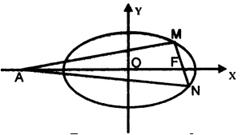
 椭圆
椭圆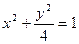 短轴的左右两个端点分别为A,B,直线
短轴的左右两个端点分别为A,B,直线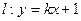 与x轴、y轴分别交于两点E,F,交椭圆于两点C,D。
与x轴、y轴分别交于两点E,F,交椭圆于两点C,D。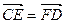 ,求直线
,求直线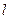 的方程;
的方程;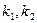 ,若
,若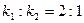 ,求k的值。
,求k的值。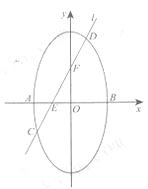
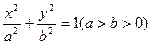 的离心率为
的离心率为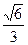 ,长轴长为
,长轴长为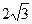 ,直线
,直线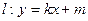 交椭圆于不同的两点A、B。
交椭圆于不同的两点A、B。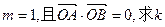 的值(O点为坐标原点);
的值(O点为坐标原点);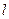 的距离为
的距离为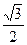 ,求
,求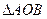 面积的最大值。
面积的最大值。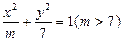 上一点P到右焦点的距离是长轴两端点到右焦点距离的等差中项,则P点的坐标为 .
上一点P到右焦点的距离是长轴两端点到右焦点距离的等差中项,则P点的坐标为 .  、
、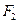 分别是椭圆
分别是椭圆 的左、右焦点.
的左、右焦点. 
 的最大值和最小值;
的最大值和最小值;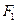 为椭圆的左焦点,
为椭圆的左焦点,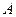 、
、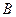 分别为椭圆的右顶点和上顶点,
分别为椭圆的右顶点和上顶点,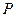 为椭圆上的点,当
为椭圆上的点,当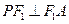 ,
,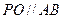 (
(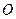 为椭圆的中心)时,椭圆的离心率为 .
为椭圆的中心)时,椭圆的离心率为 .