题目内容
工厂生产某种产品，次品率p与日产量x（万件）间的关系为p＝
，（c为常数， 且0<c<6）．已知每生产1件合格产品盈利3元，每出现1件次品亏损1．5元．
⑴将日盈利额y（万元）表示为日产量x（万件）的函数；
⑵为使日盈利额最大，日产量应为多少万件？（注：次品率＝
×100%）
解：⑴当x>c时，p＝
，y＝
·x·3－·x·
＝0；………………………… （2分）
当0<x≤c时，p＝
，
∴y＝
·x·3－·x·＝
．………………………………… （4分）
∴日盈利额y（万元）与日产量x（万件）的函数关系为
y＝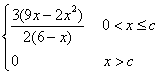
………………………………………………………（6分）
⑵由⑴知，当x>c时，日盈利额为0．
当0<x≤c时，
∵y＝，
∴y′＝
＝
，…………………………………………………………………（8分）
令y′＝0，得x＝3或x＝9（舍去）．
∴①当0<c<3时，∵y′>0，∴y在区间（0，c]上单调递增，
∴y最大值＝f（c）＝
……………………………………………………（10分）
②当3≤c＜6时，在（0,3）上，y′＞0，在（3，c）上y′＜0，
∴y在（0,3）上单调递增，在（3，c）上单调递减．
∴y最大值＝f（3）＝
． （12分）
综上，若0＜c＜3，则当日产量为c万件时，日盈利额最大；
若3≤c＜6，则当日产量为3万件时，日盈利额最大． （13分）
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
，已知生产一件合格产品能盈利25万元，生产一件次品次亏损10万元，假设该产品任何两件之间合格与否相互没有影响。
与月份
的关系，模拟的函数可以选用二次函数
（
为常数，且
）或函数
（
为常数，且
）。已知4月份该产品的产量为
万件，请问用以上哪个函数作为模拟函数较好，并说明理由。