题目内容
三角形ABC中，角A、B、C的对边分别是a，b，c，且a＞b＞c，a2＜b2+c2，则角A的取值范围是（ ）A．（
，π）B．（
，
）C．（
，
）D．（0，
）
【答案】分析：由条件推出A为锐角，从而判断△ABC的形状，通过a＞b＞c，推出A的范围．
解答：解：△ABC中，由a＞b＞c，说明A最大，由a2＜b2+c2 ，故A为锐角，
故△ABC的形状是锐角三角形，因为A最大，所以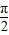A＜
，A∈（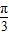
，
）
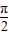故选C．
点评：本题主要考查三角形的形状的方法，勾股定理（或余弦定理）的应用，属于中档题．
解答：解：△ABC中，由a＞b＞c，说明A最大，由a2＜b2+c2 ，故A为锐角，
故△ABC的形状是锐角三角形，因为A最大，所以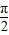A＜
，A∈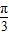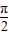（，）故选C．
点评：本题主要考查三角形的形状的方法，勾股定理（或余弦定理）的应用，属于中档题．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
在不等边三角形ABC中，角A，B，C所对的边分别为a，b，c，a为最大边，如果sin2（B+C）＜sin2B+sin2C，则角A的取值范围为（ ）
A、（0，
| ||||
B、（
| ||||
C、（
| ||||
D、（
|