题目内容
在不等边三角形ABC中,角A,B,C所对的边分别为a,b,c,a为最大边,如果sin2(B+C)<sin2B+sin2C,则角A的取值范围为( )
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
分析:先根据题意得到sin2A<sin2B+sin2C,结合正弦定理可得到a2<b2+c2,再由余弦定理可判断cosA>0,进而可判断0<A<
,再由 a为最大边可得到A为最大角,进一步可确定A的范围.
| π |
| 2 |
解答:解:由题意得:sin2A<sin2B+sin2C,
再由正弦定理得a2<b2+c2,即b2+c2-a2>0.
则cosA=
>0,∵0<A<π,∴0<A<
.
又a为最大边,∴A>
.
因此得角A的取值范围是(
,
).
故选D.
再由正弦定理得a2<b2+c2,即b2+c2-a2>0.
则cosA=
| b2+c2-a2 |
| 2bc |
| π |
| 2 |
又a为最大边,∴A>
| π |
| 3 |
因此得角A的取值范围是(
| π |
| 3 |
| π |
| 2 |
故选D.
点评:本题主要考查正弦定理和余弦定理的应用,在三角形中的有关题目中正弦定理和余弦定理的应用是最广泛的,考查的比较多,一定要熟练掌握公式并能够灵活应用.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
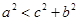 ,则A的取值范 ( )
,则A的取值范 ( )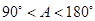 B.
B.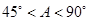 C.
C.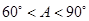 D.
D.
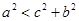 ,则A的取值范围是 ( )
,则A的取值范围是 ( )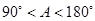 B.
B.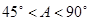 C.
C. D.
D.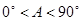
 )
) ,
, ,
, )
)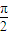 )
)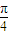 ,
, )
) ,
, )
)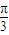 ,
,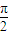 )
)