题目内容
5.已知动点A(x,y)到点(8,0)的距离定于A到点(2,0)的距离的2倍.(1)求动点A的轨迹C的方程;
(2)若直线y=kx-5与轨迹C没有公共点,求k的取值范围;
(3)求直线x+y-4=0被轨迹C截得的弦长.
分析 (1)利用动点A(x,y)到点(8,0)的距离定于A到点(2,0)的距离的2倍,建立方程,化简,可得动点A的轨迹C的方程;
(2)直线y=kx-5与x2+y2=16联立,直线y=kx-5与轨迹C没有公共点,△=100k2-36(1+k2)<0,即可求k的取值范围;
(3)求出圆心(0,0)到直线x+y-4=0的距离,即可求直线x+y-4=0被轨迹C截得的弦长.
解答 解:(1)∵动点A(x,y)到点(8,0)的距离定于A到点(2,0)的距离的2倍,
∴$\sqrt{(x-8)^{2}+{y}^{2}}$=2$\sqrt{(x-2)^{2}+{y}^{2}}$,
∴x2+y2=16;
(2)直线y=kx-5与x2+y2=16联立,可得(1+k2)x2-10kx+9=0,
∵直线y=kx-5与轨迹C没有公共点,
∴△=100k2-36(1+k2)<0,
∴-$\frac{3}{4}$<k<$\frac{3}{4}$;
(3)圆心(0,0)到直线x+y-4=0的距离为2$\sqrt{2}$,
∴直线x+y-4=0被轨迹C截得的弦长为2$\sqrt{16-8}$=4$\sqrt{2}$.
点评 本题考查轨迹方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,确定轨迹方程是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线方程是3x±4y=0,则此双曲线的离心率是( )
| A. | $\frac{4}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{2}$ |
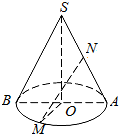 已知圆锥的底面半径r=2,半径OM与母线SA垂直,N是SA中点,NM与高SO所成的角为α,tanα=2.则圆锥的体积为$\frac{4\sqrt{5}}{3}π$.
已知圆锥的底面半径r=2,半径OM与母线SA垂直,N是SA中点,NM与高SO所成的角为α,tanα=2.则圆锥的体积为$\frac{4\sqrt{5}}{3}π$.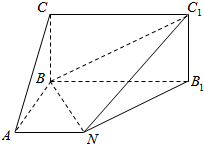 如图,矩形BB1C1C所在平面与底面ANB1B垂直,在直角梯形ANB1B中,AB⊥AN,CB=BA=AN=4,BB1=8,AN∥BB1.
如图,矩形BB1C1C所在平面与底面ANB1B垂直,在直角梯形ANB1B中,AB⊥AN,CB=BA=AN=4,BB1=8,AN∥BB1.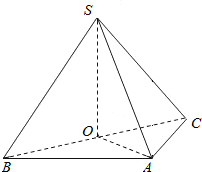 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°.