题目内容
16.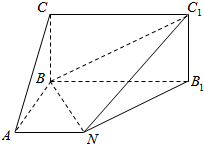 如图,矩形BB1C1C所在平面与底面ANB1B垂直,在直角梯形ANB1B中,AB⊥AN,CB=BA=AN=4,BB1=8,AN∥BB1.
如图,矩形BB1C1C所在平面与底面ANB1B垂直,在直角梯形ANB1B中,AB⊥AN,CB=BA=AN=4,BB1=8,AN∥BB1.(Ⅰ)求直线AB和C1N所成的角的余弦值;
(Ⅱ)求证:BN⊥平面C1B1N;
(Ⅲ)求BB1与平面C1BN所成角的正弦值.
分析 (Ⅰ)建立空间直角坐标系,根据向量的夹角公式即可求出直线AB和C1N所成的角的余弦值,
(Ⅱ)根据${\overrightarrow{N{B}_{1}}}_{\;}$•$\overrightarrow{BN}$=0,$\overrightarrow{BN}$•$\overrightarrow{{B}_{1}{C}_{1}}$=0得到B1N⊥BN,BN⊥B1C1,然后证明BN⊥平面C1B1N,
(Ⅲ)求出平面C1BN法向量,设BB1与平面C1BN所成角的角为α,$\overrightarrow{B{B}_{1}}$与向量为$\overrightarrow{n}$的夹角为β,根据向量的夹角公式求解即可.
解答 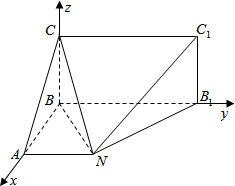 解:(I)以BA,BB1,BC分别为x,y,z轴建立空间直角坐标系,
解:(I)以BA,BB1,BC分别为x,y,z轴建立空间直角坐标系,
则B(0,0,0),A=(4,0,0),N(4,4,0),B1(0,8,0),C1(0,8,4),C(0,0,4),
∴$\overrightarrow{BA}$=(4,0,0),$\overrightarrow{{C}_{1}N}$=(4,-4,-4),
∴$\overrightarrow{BA}$•$\overrightarrow{{C}_{1}N}$=16,|$\overrightarrow{BA}$|=4,|$\overrightarrow{{C}_{1}N}$|=4$\sqrt{3}$,
设直线AB和C1N所成的角为θ,
∴cosθ=$\frac{\overrightarrow{BA}•\overrightarrow{{C}_{1}N}}{|\overrightarrow{BA}||\overrightarrow{{C}_{1}N}|}$=$\frac{16}{4×4\sqrt{3}}$=$\frac{\sqrt{3}}{3}$;
(Ⅱ)由(Ⅰ)知${\overrightarrow{N{B}_{1}}}_{\;}$=(-4,4,0),$\overrightarrow{BN}$=(4,4,0),$\overrightarrow{{B}_{1}{C}_{1}}$=(0,0,4)
∴${\overrightarrow{N{B}_{1}}}_{\;}$•$\overrightarrow{BN}$=0,$\overrightarrow{BN}$•$\overrightarrow{{B}_{1}{C}_{1}}$=0,
∴BN⊥NB1,BN⊥B1C1,
∵NB1∩B1C1=B1,
∴BN⊥平面C1B1N.
(Ⅲ)∵$\overrightarrow{B{B}_{1}}$=(0,8,0),$\overrightarrow{B{C}_{1}}$=(0,8,4)
设平面法平面C1BN向量为$\overrightarrow{n}$=(x,y,z),
则$\overrightarrow{n}$•$\overrightarrow{BN}$=0,$\overrightarrow{n}$•$\overrightarrow{B{C}_{1}}$=0,
即$\left\{\begin{array}{l}{4x+4y=0}\\{8y+4z=0}\end{array}\right.$,
∴$\overrightarrow{n}$=(1,-1,2),
∴$\overrightarrow{n}$•$\overrightarrow{B{B}_{1}}$=-8,|$\overrightarrow{B{B}_{1}}$|=8,|$\overrightarrow{n}$|=$\sqrt{6}$,
设BB1与平面C1BN所成角的角为α,$\overrightarrow{B{B}_{1}}$与向量为$\overrightarrow{n}$的夹角为β,
∴sinα=|cosβ|=|$\frac{\overrightarrow{B{B}_{1}}•\overrightarrow{n}}{|\overrightarrow{B{B}_{1}}||\overrightarrow{n}|}$|=$\frac{8}{8×\sqrt{6}}$=$\frac{\sqrt{6}}{6}$.
点评 本题考查空间向量的应用,直线与平面垂直的判定定理的应用,线面角,线线角的求法,考查计算能力以及逻辑推理能力,属于中档题.

| A. | 150° | B. | 120° | C. | 60°或120° | D. | 30°或150° |
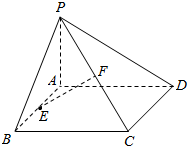 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E,F分别是AB,PC的中点,AB=$\frac{1}{2}$AD=1.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E,F分别是AB,PC的中点,AB=$\frac{1}{2}$AD=1.