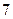题目内容
设F1,F2是椭圆E:
+2y2=1(a>
)的左右焦点,过F1的直线l与E相交于A、B两点,且|AF2|,|AB|,|BF2|成等差数列
(1)求|AB|;
(2)若直线l的斜率为1,求椭圆E的方程.
| x2 |
| a2 |
| ||
| 2 |
(1)求|AB|;
(2)若直线l的斜率为1,求椭圆E的方程.
(1)由|AF2|,|AB|,|BF2|成等差数列,
得2|AB|=|AF2|+|BF2|,由椭圆定义知|AF2|+|AB|+|BF2|=4a.
所以3|AB|=4a,|AB|=
a;
(2)由题意设直线l的方程为y=x+c.
联立
,得(2a2+1)x2+4a2cx+2a2c2-a2=0
则x1+x2=
,x1x2=
.
所以|AB|=
=
=
=
.
解得:a2=2.
代入△满足△>0成立.
所以椭圆方程为
+2y2=1.
得2|AB|=|AF2|+|BF2|,由椭圆定义知|AF2|+|AB|+|BF2|=4a.
所以3|AB|=4a,|AB|=
| 4 |
| 3 |
(2)由题意设直线l的方程为y=x+c.
联立
|
则x1+x2=
| -4a2c |
| 2a2+1 |
| 2a2c2-a2 |
| 2a2+1 |
所以|AB|=
| 2 |
| (x1+x2)2-4x1x2 |
=
| 2 |
(-
|
=
| 2 |
|
| 4a |
| 3 |
解得:a2=2.
代入△满足△>0成立.
所以椭圆方程为
| x2 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
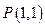 作直线
作直线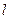 ,使得它被椭圆
,使得它被椭圆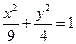 所截出的弦的中点恰为
所截出的弦的中点恰为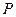 ,则直线
,则直线