题目内容
5. 在长方体ABCD-A1B1C1D1中,底面边长AB=3m,BC=4m,高BB1=5m,求:
在长方体ABCD-A1B1C1D1中,底面边长AB=3m,BC=4m,高BB1=5m,求:(1)写出B1D、BC1在平面ABCD内的射影;
(2)对角线DB1与平面ABCD所成角的大小;
(3)BC1与平面ABCD所成角的正切.
分析 (1)由B1B⊥平面ABCD,垂足为B,C1C⊥平面ABCD,垂足为C,能求出B1D、BC1在平面ABCD内的射影.
(2)由B1B⊥平面ABCD,得∠B1DB是对角线DB1与平面ABCD所成角,由此能求出对角线DB1与平面ABCD所成角的大小.
(3)由C1C⊥平面ABCD,得∠C1BC是BC1与平面ABCD所成角,由此能求出BC1与平面ABCD所成角的正切.
解答 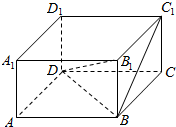 解:(1)∵B1B⊥平面ABCD,垂足为B,
解:(1)∵B1B⊥平面ABCD,垂足为B,
∴B1D在平面ABCD内的射影为BD;
∵C1C⊥平面ABCD,垂足为C,
∴BC1在平面ABCD内的射影为BC.
(2)∵B1B⊥平面ABCD,垂足为B,B1D在平面ABCD内的射影为BD,
∴∠B1DB是对角线DB1与平面ABCD所成角,
∵在长方体ABCD-A1B1C1D1中,底面边长AB=3m,BC=4m,高BB1=5m,
∴BD=$\sqrt{9+16}$=5(m),
∴tan∠B1DB=$\frac{B{B}_{1}}{BD}$=$\frac{5}{5}$=1,∴∠B1DB=45°,
∴对角线DB1与平面ABCD所成角的大小为45°.
(3)∵C1C⊥平面ABCD,垂足为C,BC1在平面ABCD内的射影为BC,
∴∠C1BC是BC1与平面ABCD所成角,
tan∠C1BC=$\frac{C{C}_{1}}{BC}$=$\frac{5}{4}$,
∴BC1与平面ABCD所成角的正切为$\frac{5}{4}$.
点评 本题考查直线在平面中的射影的求法,考查线面的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
16.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{1}{3}$+π | B. | $\frac{2}{3}$+2π | C. | $\frac{8}{3}$+8π | D. | $\frac{4}{3}$+4π |
20.函数$y={log_{\frac{1}{2}}}(3x-2)$的定义域是( )
| A. | $(\frac{2}{3},+∞)$ | B. | (1,+∞) | C. | $[{\frac{2}{3},1}]$ | D. | $(\frac{2}{3},\left.1]$ |
10.两个圆锥的母线长相等,侧面展形圆心角分别为120°和240°,体积分别为V1和V2,则V1:V2等于( )
| A. | 1:8 | B. | 1:10 | C. | $\sqrt{10}$:10 | D. | $\sqrt{5}$:5 |
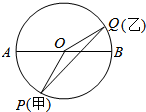 如图,有一个半径为20m的圆形水池,甲、乙两人分别从水池一条直径AB的两端开始,同时按逆时针方向绕水池边缘做匀速圆周运动,已知乙绕水池2圈需要1min,甲的速度是乙的两倍.如果从两人出发时开始计时,求当乙绕水池1周的过程中,两人的直线距离l(m)和时间t(s)的函数关系式.
如图,有一个半径为20m的圆形水池,甲、乙两人分别从水池一条直径AB的两端开始,同时按逆时针方向绕水池边缘做匀速圆周运动,已知乙绕水池2圈需要1min,甲的速度是乙的两倍.如果从两人出发时开始计时,求当乙绕水池1周的过程中,两人的直线距离l(m)和时间t(s)的函数关系式.