题目内容
设函数 .
.
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ)设函数 ,若当
,若当 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(Ⅰ)解:因为 ,其中
,其中 . 所以
. 所以 ,
,
当 时,
时, ,所以
,所以 在
在 上是增函数
上是增函数
当 时,令
时,令 ,得
,得
所以 在
在 上是增函数,在
上是增函数,在 上是减函数.
上是减函数.
(Ⅱ)解:令 ,则
,则 ,
,
根据题意,当 时,
时, 恒成立.
恒成立.
所以
(1)当 时,
时, 时,
时, 恒成立.
恒成立.
所以 在
在 上是增函数,且
上是增函数,且 ,所以不符题意…………10分
,所以不符题意…………10分
(2)当 时,
时, 时,
时, 恒成立.
恒成立.
所以 在
在 上是增函数,且
上是增函数,且 ,所以不符题意………………12分
,所以不符题意………………12分
(3)当 时,
时, 时,恒有
时,恒有 ,故
,故 在
在 上是减函数,
上是减函数,
于是“ 对任意
对任意 都成立”的充要条件是
都成立”的充要条件是 ,
,
即 ,解得
,解得 ,故
,故 .
.
综上所述, 的取值范围是
的取值范围是 .
.

练习册系列答案
相关题目
 中,
中, ,
, ,当
,当 时,
时, 等于
等于 的个位数,若数列
的个位数,若数列 项和为243,则
项和为243,则 的焦距为2,以O为圆心,
的焦距为2,以O为圆心,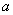 为半径的圆,过点
为半径的圆,过点 作圆的两切线互相垂直,则离心率
作圆的两切线互相垂直,则离心率 = 。
= 。 ,若存在实数
,若存在实数 ,使得
,使得 成立,则实数
成立,则实数 的取值范围是( ) w
的取值范围是( ) w B.
B. C.
C. D.
D.
 表示的平面区域是三角形, 则实数
表示的平面区域是三角形, 则实数 的取值范围是 .
的取值范围是 .  到直线
到直线 的角为
的角为 ,则实数
,则实数 的值等
的值等 于 ( )
于 ( ) C.0或
C.0或
 满足下列两个条件:
满足下列两个条件: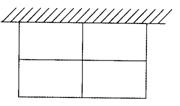
 中,
中, 等于( )
等于( )