题目内容
7.若正方体A1A2A3A4-B1B2B3B4的棱长为1,则集合{x|x=$\overrightarrow{{A}_{1}{B}_{1}}$•$\overrightarrow{{A}_{i}{B}_{j}}$,i∈{1,2,3,4},j∈1,2,3,4}}中元素的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 $\overrightarrow{{A}_{1}{B}_{1}}$⊥$\overrightarrow{{A}_{i}{B}_{j}}$,$\overrightarrow{{A}_{2}{B}_{1}}$⊥$\overrightarrow{{B}_{1}{B}_{j}}$,i,j∈{1,2,3,4},由此能求出集合{x|x=$\overrightarrow{{A}_{1}{B}_{1}}$•$\overrightarrow{{A}_{i}{B}_{j}}$,i∈{1,2,3,4},j∈1,2,3,4}}中元素的个数.
解答 解:∵正方体A1A2A3A4-B1B2B3B4的棱长为1,
$\overrightarrow{{A}_{1}{B}_{1}}$⊥$\overrightarrow{{A}_{i}{B}_{j}}$,$\overrightarrow{{A}_{2}{B}_{1}}$⊥$\overrightarrow{{B}_{1}{B}_{j}}$,i,j∈{1,2,3,4},
∴$\overrightarrow{{A}_{1}{B}_{1}}$•$\overrightarrow{{A}_{i}{B}_{j}}$=$\overrightarrow{{A}_{1}{B}_{1}}$•($\overrightarrow{{A}_{i}{A}_{1}}$+$\overrightarrow{{A}_{1}{B}_{1}}$+$\overrightarrow{{B}_{1}{B}_{j}}$)
=$\overrightarrow{{A}_{1}{B}_{1}}$•$\overrightarrow{{A}_{j}{A}_{1}}$+${\overrightarrow{{A}_{1}{B}_{1}}}^{2}$+$\overrightarrow{{A}_{1}{B}_{1}}•\overrightarrow{{B}_{1}{B}_{j}}$=1.
∴集合{x|x=$\overrightarrow{{A}_{1}{B}_{1}}$•$\overrightarrow{{A}_{i}{B}_{j}}$,i∈{1,2,3,4},j∈1,2,3,4}}中元素的个数为1.
故选:A.
点评 本题考查的知识点是集合中元素个数的求法,向量数量积的应用,难度不大,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 4 | B. | 1 | C. | 18 | D. | $\frac{4}{5}$ |
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $\frac{28}{3}$ | B. | $\frac{19}{2}$ | C. | 6 | D. | 2$\sqrt{10}$+3 |
| A. | $\frac{18}{35}$ | B. | $\frac{15}{35}$ | C. | $\frac{12}{35}$ | D. | $\frac{9}{35}$ |
| A. | b<a<c | B. | a<b<c | C. | b<c<a | D. | c<a<b |
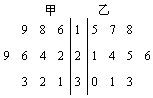 甲、乙两人在10天中每天加工零件的个数用茎叶图表示如图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数.则这十天甲、乙两人每人每日加工零件的平均数的和为49.
甲、乙两人在10天中每天加工零件的个数用茎叶图表示如图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数.则这十天甲、乙两人每人每日加工零件的平均数的和为49.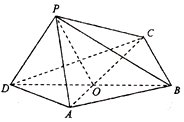 如图,四边形ABCD中,△BCD为正三角形,AD=AB=2,BD=2$\sqrt{3}$,AC与BD交于O点.将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为θ,且P点在平面ABCD内的射影落在△ACD内.
如图,四边形ABCD中,△BCD为正三角形,AD=AB=2,BD=2$\sqrt{3}$,AC与BD交于O点.将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为θ,且P点在平面ABCD内的射影落在△ACD内.