Question

【题目】已知函数

（1）若函数在区间上恒成立，求实数a的取值范围；

（2）若函数在区间上有两个极值点，求实数a的取值范围；

（3）若函数的导函数的图象与函数图象有两个不同的交点，求实数a的取值范围．

Answer 1

【答案】（1）；（2）；（3）.

【解析】

（1）在区间上恒成立等价于当时，恒成立，利用导数判断函数在上的单调性求出最大值即可得解；（2）求出导数，则在区间上有两个不同零点，根据二次函数的图象与性质列出不等式组求a的取值范围，取，，判断函数单调性验证，分别为极大值与极小值即可；（3）题意等价于函数有两个零点，分析函数单调性知，再根据为函数的极值点即可代入不等式求出的范围从而求出a的范围，再验证函数的两个零点.

（1）

即当时，恒成立，

设

，

因为，所以，在上单调递增，

所以，所以，．

（2）因为，

所以在区间上有两个极值点的必要条件为

在区间上有两个不同零点，

则，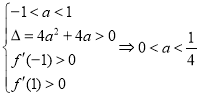

当时，在上递减，在上递增

，，

所以存在唯一的，使得，

因为在区间大于零，在区间小于零，在区间上大于零，

所以在区间上递增，在区间上递减，在上递增，

所以，分别为极大值与极小值，

所以当时函数在区间上有两个极值点；

（3）因为

所以，

令，，

令，解得（舍去），.

		0	＋
	↓	极小值	↑

因为有两个零点，

所以，①

又因为，所以②

代入①得到，

令，

所以在上递减，因为，所以，

因为在区间上递增，所以．

i）因为，所以，

，

令，，

所以

所以在上递增，，所以

所以在区间上存在唯一一个零点．

ⅱ）又因为

，

且，

所以在区间上存在唯一一个零点，

综上时，的图像与图像有两个不同的交点．

解法二：由

得

令，

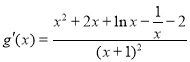
令，．

，所以当时，，

当时，，即当时，，

当时，，

所以在区间上递减，在区间上递增，

所以即，

i）当时，因为

所以

取，则

所以在区间上存在唯一一个零点，

ii）当时，

令，

因为，，

所以，所以在上递增，

，所以，即

所以在区间上存在唯一一个零点，

综上时，的图像与图像有两个不同的交点.