题目内容

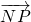如图所示，已知圆C：（x+1）²+y²=8，定点A（1，0），M为圆上一动点，点P在AM上，点N在CM上，且满足 $数学公式$ =2 $数学公式$ ， $数学公式$ • $数学公式$ =0，点N的轨迹方程是

A.
$数学公式$ +y²=1
B.
$数学公式$ -y²=1
C.
x²+ $数学公式$ =1
D.
x²- $数学公式$ =1

A
分析：利用线段垂直平分线的性质推出 NC+NM=r=2 $\text{[math]}$ ＞AC，再利用椭圆的定义知，点N的轨迹是以A、C 为焦点的椭圆，利用待定系数法求出椭圆的方程．
解答：解：C（-1，0），∵ $\text{[math]}$ =2 $\text{[math]}$ ，∴P 为AM的中点．∵ $\text{[math]}$ =0，∴NP⊥AM．
故 NP为线段AM的中垂线，∴NM=NA．∵NM+NC=2 $\text{[math]}$ （半径），
所以CN+AN=CM=2 $\text{[math]}$ ，故N点轨迹为以A、C为焦点的椭圆，有
c=1，a= $\text{[math]}$ ，可得b=1，故
点N轨迹方程曲线E为 $\text{[math]}$ +y²=1，
故选A．
点评：本题考查轨迹方程的求法，椭圆的定义，判断点N的轨迹是以A、C为焦点的椭圆，是解题的关键．

练习册系列答案

全能练考卷系列答案

随堂优化训练系列答案

王朝霞培优100分系列答案

无敌战卷系列答案

小学生绩优名卷系列答案

一课一练课时达标系列答案

新课标同步课堂优化指导系列答案

新课程新设计名师同步导学系列答案

英才计划周测月考期中期末系列答案

与名师对话系列答案

相关题目

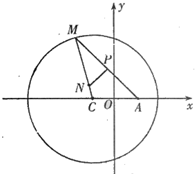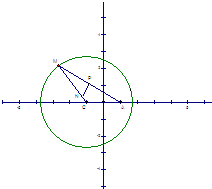如图所示，已知圆C：（x+1）²+y²=8，定点A（1，0），M为圆C上一动点，点P在线段AM上，点N在线段CM上，且满足

=0，点N的轨迹为曲线E．
（1）求曲线E的方程；
（2）若过定点F（0，2）的直线交曲线E于不同的两点G、H（点G在点F、H之间），且满足

，求λ的取值范围．

（理）如图所示，已知圆C：（x+1）²+y²=8，定点A（1，0），M为圆上一动点，点P在AM上，点N在CM上，且满足

=0，点N的轨迹为曲线E．
（1）求曲线E的方程；
（2）过点S（0，

）且斜率为k的动直线l交曲线E于A、B两点，在y轴上是否存在定点G，满足

使四边形NAPB为矩形？若存在，求出G的坐标和四边形NAPB面积的最大值；若不存在，说明理由．

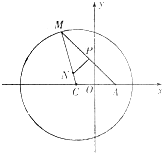如图所示，已知圆C：（x+1）²+y²=8，定点A（1，0），M为圆上一动点，点P在AM上，点N在CM上，且满足AM=2AP，NP⊥AM，点N的轨迹为曲线E．
（1）求曲线E的方程；
（2）若过定点F（0，2）的直线l交曲线E于不同的两点G、H（点G在点F、H之间），且满足FG=

FH，求直线l的方程；
（3）设曲线E的左右焦点为F₁，F₂，过F₁的直线交曲线于Q，S两点，过F₂的直线交曲线于R，T两点，且QS⊥RT，垂足为W；
（ⅰ）设W（x₀，y₀），证明：

＜1；
（ⅱ）求四边形QRST的面积的最小值．

（2006•石景山区一模）如图所示，已知圆C：（x+1）²+y²=8，定点A（1，0），M为圆上一动点，点P在AM上，点N在CM上，且满足

=0，点N的轨迹为曲线E．
（Ⅰ）求曲线E的方程；
（Ⅱ）若点B₁（x₁，y₁），B₂（-1，y₂），B₃（x₃，y₃）在曲线E上，线段B₁B₃的垂直平分线为直线l，且|B₁A|，|B₂A|，|B₃A|成等差数列，求x₁+x₃的值，并证明直线l过定点；
（Ⅲ）若过定点F（0，2）的直线交曲线E于不同的两点G、H（点G在点F、H之间），且满足

，求λ的取值范围．

如图所示，已知圆C：（x+1）²+y²=8，定点A（1，0），M为圆上一动点，点P在AM上，点N在CM上，且满足

=0，点N的轨迹方程是（　　）