题目内容
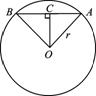
1弧度的圆心角所对弦长为2，求此圆心角所夹扇形的面积.
解析：设扇形所在圆的半径为r，则1弧度所对的弧度长为r,由AB=2，在Rt△AOC中，r=OA=
,
∴S扇形=
r2=
=
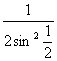csc2
.
温馨提示
要求掌握弧长公式l=α·r和扇形面积公式S=
×l×r,记忆时可与三角形的面积公式S=
×底×高统一起来.
练习册系列答案
相关题目
若1弧度的圆心角所对的弦长等于2，则这圆心角所对的弧长等于（ ）
A、sin
| ||||
B、
| ||||
C、
| ||||
D、2sin
|
如果1弧度的圆心角所对的弦长为2，那么这个圆心角所对的弧长为（ ）
A、
| ||
| B、sin0.5 | ||
| C、2sin0.5 | ||
| D、tab0.5 |
B.
D．2sin