题目内容
1.如果函数f(x)=$\sqrt{x+2}$+a-x存在两个不同的零点,则实数a的取值范围是( )| A. | (-$\frac{9}{4}$,+∞) | B. | (-$\frac{9}{4}$,-2] | C. | [-2,+∞) | D. | (-$\frac{9}{4}$,0) |
分析 移项,两边平方,问题转化为g(x)=x2-(2a+1)x+a2-2=0两根需大于等于a,即可求出实数a的取值范围.
解答 解:f(x)=$\sqrt{x+2}$+a-x=0,∴$\sqrt{x+2}$=x-a,x≥a
平方得:x+2=x2-2ax+a2,
设g(x)=x2-(2a+1)x+a2-2=0
△=4a2+4a+1-4a2+8=4a+9>0,∴a>-$\frac{9}{4}$.
∵两根需大于等于a,
∴二次曲线的对称轴为:x=$\frac{2a+1}{2}$>a,g(a)=a2-(2a+1)a+a2-2=-a-2≥0,∴a≤-2
因此综合得:-$\frac{9}{4}$<a≤-2.
故选:B.
点评 本题考查求实数a的取值范围,考查学生分析解决问题的能力,正确转化是关键.

练习册系列答案
相关题目
5.函数f(x)=loga$\frac{2x+1}{x-1}$-3的图象必过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.以直线x±2y=0为渐近线,且截直线x-y-3=0所得弦长为$\frac{8\sqrt{3}}{3}$的双曲线方程为( )
| A. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{8}$=1 | B. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{4}$=1 | C. | y2-$\frac{{x}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$-y2=1 |
16.一个水平放置的图形的斜二测直观图是底角为45°,腰和上底均为1的等腰梯形,则原图形的面积为( )
| A. | $\frac{\sqrt{2}+1}{2}$ | B. | $\sqrt{2}$+1 | C. | $\frac{2+\sqrt{2}}{2}$ | D. | $\sqrt{2}$+2 |
6.等比数列{an}的首项为1,若4a1,2a2,a3成等差数列,则数列{$\frac{1}{{a}_{n}}$}的前5项的和为( )
| A. | 31 | B. | $\frac{31}{16}$ | C. | $\frac{31}{32}$ | D. | $\frac{15}{8}$ |
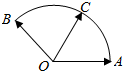 给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°.如图所示,点C在以O为圆心的圆弧AB上变动.若$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$,其中x,y∈R,则$x+\frac{5}{2}y$的最大值是$\sqrt{13}$.
给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°.如图所示,点C在以O为圆心的圆弧AB上变动.若$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$,其中x,y∈R,则$x+\frac{5}{2}y$的最大值是$\sqrt{13}$.