题目内容
(本小题满分14分)已知各项均为正数的数列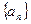 满足
满足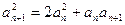 ,且
,且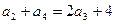 ,其中
,其中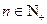 .
.
(Ⅰ)求数列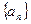 的通项公式;
的通项公式;
(Ⅱ)设数列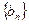 的前
的前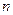 项和为
项和为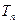 ,令
,令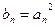 ,其中
,其中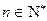 ,试比较
,试比较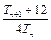 与
与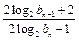 的大小,并加以证明.
的大小,并加以证明.
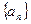 满足
满足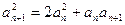 ,且
,且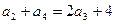 ,其中
,其中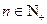 .
.(Ⅰ)求数列
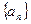 的通项公式;
的通项公式;(Ⅱ)设数列
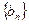 的前
的前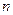 项和为
项和为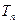 ,令
,令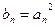 ,其中
,其中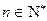 ,试比较
,试比较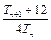 与
与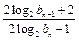 的大小,并加以证明.
的大小,并加以证明.(Ⅰ)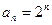
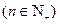
(Ⅱ)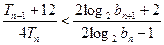
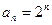
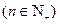
(Ⅱ)
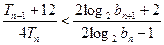
(Ⅰ)因为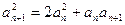 ,即
,即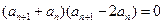 ………2分
………2分
又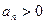 ,所以有
,所以有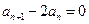 ,所以
,所以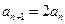 …………3分
…………3分
所以数列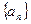 是公比为
是公比为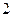 的等比数列,由
的等比数列,由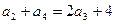 得
得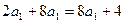 ,解得
,解得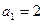 ……4分
……4分
故数列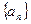 的通项公式为
的通项公式为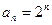
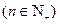 …………5分
…………5分
(Ⅱ)因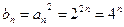 ,………6分,所以
,………6分,所以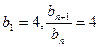
即数列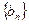 是首项为
是首项为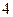 ,公比是
,公比是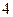 的等比数列,所以
的等比数列,所以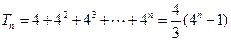 …………7分
…………7分
则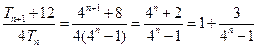 ,又
,又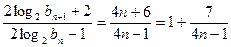
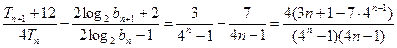 ………9分
………9分
当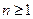 时,
时,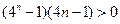
当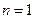 时,
时,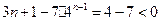 ,当
,当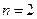 时,
时,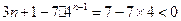
猜想: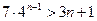 (
(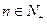 )…………10分,下面用数学归纳法证明
)…………10分,下面用数学归纳法证明
①当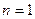 时,
时,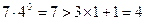 ,上面不等式显然成立;………11分
,上面不等式显然成立;………11分
②假设当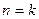 时,不等式
时,不等式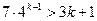 成立…………12分
成立…………12分
当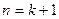 时,
时,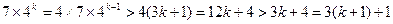 ………13分
………13分
综上①②对任意的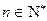 均有
均有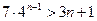
又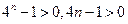 ,所以对任意的
,所以对任意的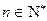 均有
均有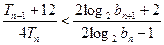 …………14分
…………14分
证明二:(Ⅱ) 因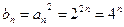 ,………6分,所以
,………6分,所以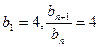
即数列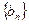 是首项为
是首项为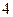 ,公比是
,公比是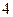 的等比数列,所以
的等比数列,所以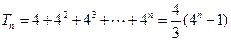 …………7分
…………7分
则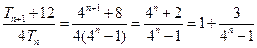 ,又
,又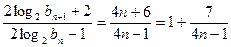
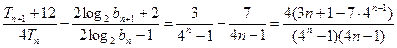 ………9分
………9分
当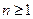 时,
时,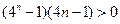 ………10分
………10分
因为 ………12分
………12分
∵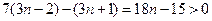 ,∴
,∴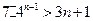 ………13分
………13分
 ,即对任意的
,即对任意的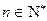 均有
均有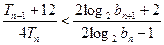 ………14分
………14分
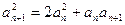 ,即
,即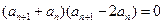 ………2分
………2分又
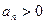 ,所以有
,所以有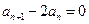 ,所以
,所以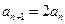 …………3分
…………3分所以数列
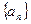 是公比为
是公比为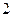 的等比数列,由
的等比数列,由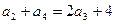 得
得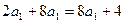 ,解得
,解得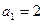 ……4分
……4分故数列
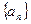 的通项公式为
的通项公式为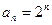
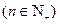 …………5分
…………5分(Ⅱ)因
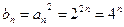 ,………6分,所以
,………6分,所以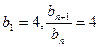
即数列
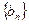 是首项为
是首项为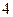 ,公比是
,公比是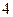 的等比数列,所以
的等比数列,所以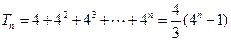 …………7分
…………7分则
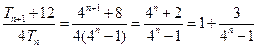 ,又
,又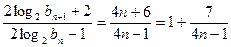
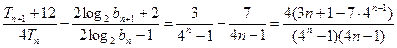 ………9分
………9分当
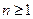 时,
时,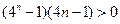
当
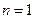 时,
时,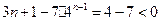 ,当
,当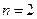 时,
时,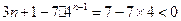
猜想:
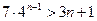 (
(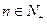 )…………10分,下面用数学归纳法证明
)…………10分,下面用数学归纳法证明①当
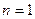 时,
时,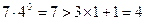 ,上面不等式显然成立;………11分
,上面不等式显然成立;………11分②假设当
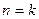 时,不等式
时,不等式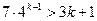 成立…………12分
成立…………12分当
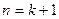 时,
时,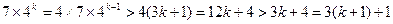 ………13分
………13分综上①②对任意的
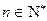 均有
均有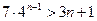
又
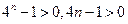 ,所以对任意的
,所以对任意的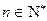 均有
均有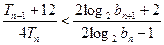 …………14分
…………14分证明二:(Ⅱ) 因
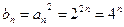 ,………6分,所以
,………6分,所以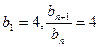
即数列
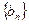 是首项为
是首项为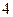 ,公比是
,公比是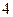 的等比数列,所以
的等比数列,所以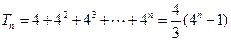 …………7分
…………7分则
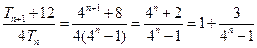 ,又
,又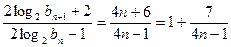
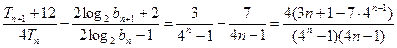 ………9分
………9分当
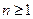 时,
时,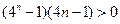 ………10分
………10分因为
 ………12分
………12分∵
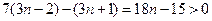 ,∴
,∴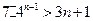 ………13分
………13分 ,即对任意的
,即对任意的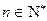 均有
均有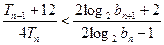 ………14分
………14分
练习册系列答案
相关题目
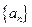 是以4为首项的正数数列,双曲线
是以4为首项的正数数列,双曲线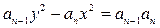 的一个焦点坐标为
的一个焦点坐标为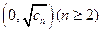 , 且
, 且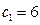 , 一条渐近线方程为
, 一条渐近线方程为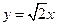 .
.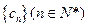 的通项公式;
的通项公式;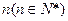 ,不等式
,不等式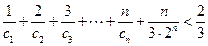 是否恒成立?并说明理由.
是否恒成立?并说明理由.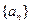 的前
的前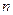 项和为
项和为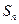 ,点
,点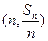 在直线
在直线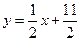 上;数列
上;数列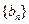 满足
满足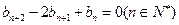 ,且
,且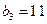 ,它的前9项和为153.
,它的前9项和为153.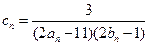 ,求数列
,求数列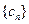 的前
的前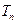 .
.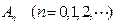 ,其中
,其中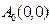 ,
,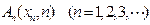 ,并且线段
,并且线段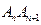 所在直线的斜率为
所在直线的斜率为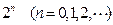 .
.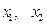
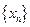 的通项公式
的通项公式
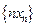 的前
的前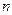 项和为
项和为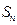 ,求
,求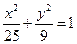 上有三点
上有三点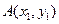 、
、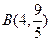 、
、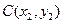 与右焦点
与右焦点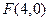 的距离成等差数列,则
的距离成等差数列,则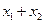 的值为( )
的值为( )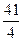
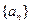 中,
中,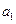 =1,
=1,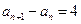 ,则
,则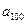 的值为 ★ .
的值为 ★ .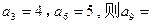
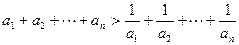 成立的最小自然数n是( )
成立的最小自然数n是( )