题目内容
(本小题满分14分)已知数列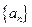 是以4为首项的正数数列,双曲线
是以4为首项的正数数列,双曲线
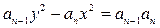 的一个焦点坐标为
的一个焦点坐标为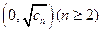 , 且
, 且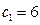 , 一条渐近线方程为
, 一条渐近线方程为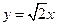 .
.
(1)求数列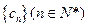 的通项公式;
的通项公式;
(2) 试判断: 对一切自然数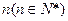 ,不等式
,不等式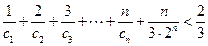 是否恒成立?并说明理由.
是否恒成立?并说明理由.
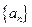 是以4为首项的正数数列,双曲线
是以4为首项的正数数列,双曲线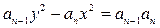 的一个焦点坐标为
的一个焦点坐标为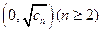 , 且
, 且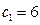 , 一条渐近线方程为
, 一条渐近线方程为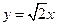 .
.(1)求数列
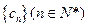 的通项公式;
的通项公式;(2) 试判断: 对一切自然数
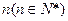 ,不等式
,不等式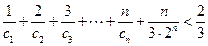 是否恒成立?并说明理由.
是否恒成立?并说明理由. ,成立
,成立解:(1)双曲线方程即为 ,所以
,所以 .………2分
.………2分
又由渐近线方程得 ,于是
,于是 . ………4分
. ………4分
∴数列 是首项为4,公比为2的等比数列,从而
是首项为4,公比为2的等比数列,从而 ,
,
∴ (n≥2). 又
(n≥2). 又 ,也符合上式,所以
,也符合上式,所以 (n∈N*).
(n∈N*).
………6分
(2)令 ①
①
则 ② ………8分
② ………8分
① -②,得
 ;
;
 , ………10分
, ………10分
∴ ,…12分
,…12分
即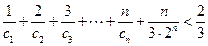 ,所以对一切自然数
,所以对一切自然数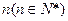 ,不等式
,不等式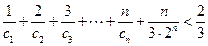 恒成立. ……14分
恒成立. ……14分
 ,所以
,所以 .………2分
.………2分又由渐近线方程得
 ,于是
,于是 . ………4分
. ………4分∴数列
 是首项为4,公比为2的等比数列,从而
是首项为4,公比为2的等比数列,从而 ,
,∴
 (n≥2). 又
(n≥2). 又 ,也符合上式,所以
,也符合上式,所以 (n∈N*).
(n∈N*).………6分
(2)令
 ①
①则
 ② ………8分
② ………8分① -②,得

 ;
; , ………10分
, ………10分∴
 ,…12分
,…12分即
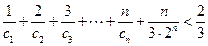 ,所以对一切自然数
,所以对一切自然数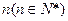 ,不等式
,不等式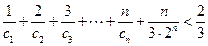 恒成立. ……14分
恒成立. ……14分
练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
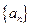 第10项为24,第25项为
第10项为24,第25项为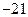 ,
,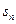 为其前n项和,求使
为其前n项和,求使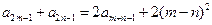
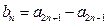 (n∈N*),证明:数列{bn}是等差数列;
(n∈N*),证明:数列{bn}是等差数列;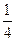
 qn-1(q≠0,n∈N*),求数列{cn}的前n项和Sn.
qn-1(q≠0,n∈N*),求数列{cn}的前n项和Sn.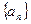 满足
满足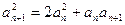 ,且
,且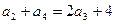 ,其中
,其中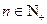 .
.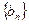 的前
的前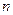 项和为
项和为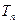 ,令
,令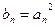 ,其中
,其中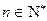 ,试比较
,试比较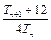 与
与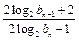 的大小,并加以证明.
的大小,并加以证明.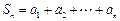 ,且
,且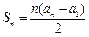 .
.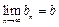 ,则称b为数列{bn}的“上渐近值”,令
,则称b为数列{bn}的“上渐近值”,令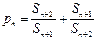 ,求数列
,求数列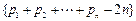 的“上渐近值”.
的“上渐近值”.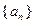 的公差是
的公差是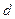 ,
,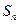 是该数列的前
是该数列的前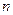 项和.
项和.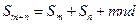 ;
;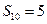 、
、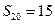 ,求
,求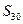 ”;
”;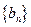 的公比为
的公比为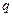 ,前
,前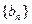 ,其中
,其中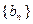 的前
的前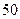 项和
项和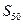 .”
.”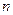 项等差数列后,仍构成一个等差数列,且新等差数列的所有项的和是781,则
项等差数列后,仍构成一个等差数列,且新等差数列的所有项的和是781,则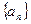 中,
中,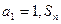 是数列
是数列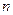 项和,对任意
项和,对任意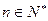 ,有
,有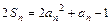 ,则数列
,则数列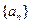 的前
的前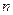 项和为
项和为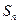 ,若
,若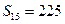 ,则
,则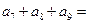 ( ).
( ).