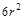题目内容
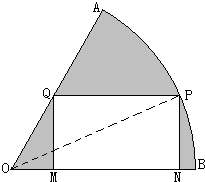 如图,在半径为R、圆心角为
如图,在半径为R、圆心角为| π | 3 |
分析:先根据已知中∠POB=a,扇形AB的,半径为R,圆心角为60°,我们易得PN=Rsinα,PQ=Rcosα-
Rsinα,代入矩形面积公式,即可得到矩形面积的表达式,结合α∈(0,
),结合三角函数的性质,我们易得,当2α+
=
时,S取最大值.
| ||
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
解答:解:∵扇形AB的半径为R,圆心角为60°
且∠POB=a,矩形PNMQ面积为S.
由题设可得S=Rsinα(Rcosα-
Rsinα).
化简得:S=
R2sin(2α+
)-
R2,α∈(0,
)
当α=
,即∠AOP=
时,
S取最大值
R2.
且∠POB=a,矩形PNMQ面积为S.
由题设可得S=Rsinα(Rcosα-
| ||
| 3 |
化简得:S=
| ||
| 3 |
| π |
| 6 |
| ||
| 6 |
| π |
| 3 |
当α=
| π |
| 6 |
| π |
| 6 |
S取最大值
| ||
| 6 |
点评:本题考查的知识点是在实际问题中建立三角函数模型,三角函数降幂公式及三角函数的最值,在本题中根据P为圆心角为60°的扇形AB弧上任一点,限制α∈(0,
)易被忽略,希望大家重视.
| π |
| 3 |

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 如图,在半径为r的圆内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设Sn为前n个圆的面积之和,则
如图,在半径为r的圆内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设Sn为前n个圆的面积之和,则| lim |
| n→∞ |
| A、2πr2 | ||
B、
| ||
| C、4πr2 | ||
| D、6πr2 |
 如图,在半径为R的圆内随机撒一粒黄豆,它落在阴影部分内接正三角形上的概率是( )
如图,在半径为R的圆内随机撒一粒黄豆,它落在阴影部分内接正三角形上的概率是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在半径为r的圆内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设Sn为前n个正六边形的面积之和,则
如图,在半径为r的圆内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设Sn为前n个正六边形的面积之和,则 为前n个圆的面积之和,则
为前n个圆的面积之和,则

 B.
B.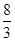
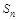 为前n
为前n 
 B.
B. C.
C. D.
D.